Модели, заданные в виде уравнений в частных производных

Ряд задач, связанных с использованием физических полей, приводит к моделям в виде дифференциальных уравнений в частных производных.

Особенностью таких задач является то, что изучаемые параметры изменяются не только во времени, но и зависят от координат x, y, z рассматриваемого пространства. Такие модели называются нестационарными. Модели, в которых параметры не зависят от времени, называются стационарными.

К таким моделям сводятся описания полей температур в элементах конструкции двигателя и полей скоростей при течении жидкости (газа). Уравнениями в частных производных описываются колебания элементов конструкции и поля напряжений, возникающих при работе этих элементов.

Линейное дифференциальное уравнение в частных производных имеет вид

.

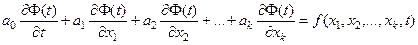Математическая модель, описанная дифференциальными уравнениями в частных производных, должна включать в себя необходимые для решения задачи краевые условия:

1. Должна быть задана область D, ограниченная поверхностью (на плоскости – кривой) G , в которой определяется решение.

2. Должны быть заданы условия на границе G этой области.

В случае нестационарного поля эти граничные условия, так же как и сама область могут меняться во времени.

Граничные условия могут быть 1-го, 2-го и 3-го рода:

а) Граничные условия 1-го рода предусматривают задание на границе величины искомой функции:

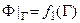– для стационарного поля;

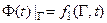– для нестационарного поля.

б) Граничные условия 2-го рода – предусматривают задание производной искомой функции:

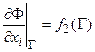– для стационарного поля;

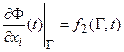– для нестационарного поля.

в) Граничные условия 3-го рода – предусматривают комбинации функции и ее производной:

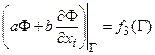– для стационарного поля;

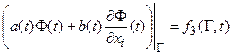– для нестационарного поля.

3. Для нестационарных полей должны быть заданы одно или два начальных условия, характеризующих состояние поля в начальный момент времени:

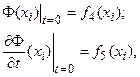(i = 1, 2, 3).

Здесь x_i – координаты пространства.

Совокупность уравнений и краевых (и начальных) условий полностью определяет модель и позволяет провести ее исследование.

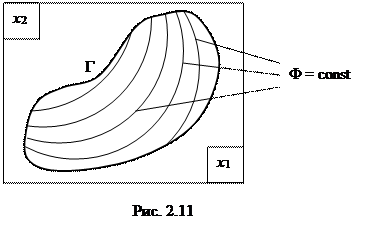
Решение часто задается в виде семейств изолиний F = const (Рис. 2.11).

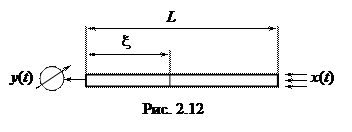
В качестве примера рассмотрим хорошо изолированный металлический пруток, нагреваемый с одной стороны. С другой стороны помещен измеритель температуры (Рис. 2.12). Величина подогрева x(t) в момент времени t является входным сигналом, а измеряемая на другом конце температура y(t) – выходным сигналом.

Обозначим через x расстояние от измерителя до точки прутка. Температура в этой точке z будет описываться функцией вида

z = z(t, x).

Уравнение теплопроводности для одномерного случая для определения функции z будет иметь вид:

,

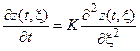где K – коэффициент теплопроводности.

Начальным условием в данном случае является начальное распределение температуры (при t = 0) по прутку: z(0, x) = j(x).

Граничные условия определяются тремя условиями:

а) Нагрев прутка на правом конце

.

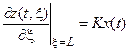б) На левом конце подвод тепла отсутствует

.

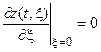в) Показания на измерителе температур (x = 0) в момент времени t определяется следующим выражением

.

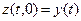Таким образом, для вычисления температуры на расстоянии L от измерителя по формуле для y(t) необходимо проинтегрировать дифференциальное уравнение с учетом начальных и граничных условий, т.е. получить функцию z(t,x). Затем следует проградуировать измеритель температуры, т.е. определить соответствие между x(t) и y(t), задавая различные значения x(t) и вычисляя .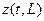

Контрольные вопросы к лекции 5

1. Где используются математические модели в виде обыкновенных дифференциальных уравнений?

2. Что должна включать в себя математическая модель в виде обыкновенных дифференциальных уравнений?

3. Какими методами осуществляется исследование моделей, заданных в виде обыкновенных дифференциальных уравнений?

4. Запишите математическую модель движения груза массой m, закрепленного на вертикальной стенке с помощью пружины жесткостью С и совершающего колебательное движение вдоль оси х в среде с вязкостью n.

5. Какой принцип используется при построении этой модели?

6. К какому типу относится эта модель?

7. Где используются математические модели в виде дифференциальных уравнений в частных производных?

8. Что является особенностью математических моделей в виде дифференциальных уравнений в частных производных?

9. Что должна включать в себя математическая модель в виде дифференциальных уравнений в частных производных?

10. Какого типа бывают граничные условия?

11. Приведите математическую модель распределения температурного поля в металлическом прутке, нагреваемом с одной стороны.