Построение математической модели сверления лазером

Примером аналитической теоретической модели может служить модель, описывающая глубину отверстия при лазерном сверлении.

Резание и сверление металлов весьма важно для многих областей техники. Значительный интерес представляет создание новых устройств, предназначенных для специальных материалов, а также для тех случаев, когда желательно обеспечить некоторую степень автоматизации указанных процессов. В последнее время для этого были предприняты попытки использования мощных лазеров.

Основная идея состоит в том, чтобы сфокусировать значительную мощность на малой площади поверхности материала, создавая таким образом интенсивный нагрев и испарение с последующим образованием отверстия. При сверлении необходимо постараться обеспечить такие условия процесса, чтобы проделанное отверстие прямо проходило сквозь материал, и избежать, таким образом, затекания расплавленного металла обратно в отверстие и застывания его там.

Построим математическую модель, главная применимость которой – глубокое сверление. При помощи модели попытаемся ответить на вопрос, как быстро можно проделать отверстие, используя пучок излучения высокой мощности, и на какую глубину.

Рассмотрим высокоэнергетический пучок лазерного излучения, сфокусированный на малом участке поверхности металла (Рис. 2.1). Определенная доля энергии поглощается, а остальная часть отражается. Поглощение энергии происходит внутри слоя, толщина которого много меньше миллиметра, вызывает поверхностный нагрев материала и рост температуры поверхности. Температура растет не безгранично. Существует два процесса, ограничивающие рост температуры:

- перенос тепла в глубь материала от нагретых к холодным участкам, обусловленный теплопроводностью;

- испарение. Когда температура материала достигает точки кипения, скрытое тепло поглощается без дальнейшего увеличения температуры в процессе испарения материала.

При удалении пара от поверхности материала в металле образуется выемка.

Задача количественного описания этого процесса и вызывает необходимость математического моделирования.

Будем рассматривать модель, описывающую процесс разрушения материала, при котором вся энергия лазерного излучения используется только для испарения материала.

Этот предельный режим испарения может возникать двумя путями:

- когда энергия поступает на поверхность слишком быстро, так что тепло не успевает распространиться в глубь металла;

- плотность мощности пучка постоянна, а распределение температуры впереди границы области испарения приближается к стационарному.

Предположим, что мощность W распределена по некоторой площади А поверхности; излучение приложено по нормали к поверхности (см. рис. 2.1). За интервал времени Dt поступает энергия W×Dt. Пусть глубина возникающей выемки равна DS, тогда объем испарившегося материала равен A×DS. Используя закон сохранения энергии, получим

h×r×A×DS = W×Dt,

где h – количество тепла, требуемое для испарения единицы массы материала; r – плотность материала.

Преобразуем это выражение и положим Dt ® 0, получим скорость роста глубины выемки:

.

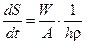Это уравнение показывает, что для любого материала предельная скорость пропорциональна плотности энерговыделения W/A. Интегрируя это уравнение и полагая S = 0 при t = 0, найдем глубину выемки в произвольный момент времени t:

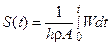(2.1)

или

,

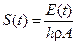где E(t) – полная энергия, выделенная источником за промежуток времени (0, t).

Таким образом, в предельном режиме испарения глубина выемки зависит только от полной энергии, поступившей на поверхность. Формула (2.1) представляет собой теоретическую аналитически-разрешимую динамическую детерминированную модель.

На практике всегда существует перенос некоторого количества тепла в материал за счет теплопроводности. Общая задача движения границы раздела фаз с учетом теплопроводности известна как задача Стефана. Ее решение представляет определенные математические трудности.

Контрольные вопросы к лекции 2

11. В виде чего может быть представлена математическая модель геометрически?

12. Что такое область определения математической модели?

13. Какая модель называется унимодальной?

14. Как задаются математические модели аналитического типа?

15. Приведите пример математической модели аналитического типа.

16. Какие задачи позволяет решить модель, заданная в явном виде?

17. Какой предельный режим рассматривается при построении математической модели сверления лазером?

18. Какой закон используется при построении математической модели сверления лазером?

19. Назовите процессы, препятствующие росту температуры при лазерном сверлении.

20. На какие вопросы можно ответить, используя математическую модель сверления лазером?

21. К какому типу принадлежит модель зависимости глубины выемки от длительности импульса?

Наиболее простыми являются так называемые линейные детерминированные модели. Они задаются в виде линейной формы управляющих переменных (х):

W = a₀ + a₁x₁ + … + a_kx_k

при линейных ограничениях вида

b_1j x₁ + b_2j x₂ + … + b_kj x_k ³ b_j , j = 1,…, q₁;

c_1j x₁ + c_2j x₂ + … + c_kj x_k = c_j , j = 1,…, q₂;

d_1j x₁ + d_2j x₂ + … + d_kj x_k £ d_j , j = 1,…, q₃.

Общее число ограничений m = q₁ + q₂ + q₃ может превосходить число переменных (m > k). Кроме того, обычно вводится условие положительности переменных (x_i ³ 0).

Поверхность отклика для линейной модели представляет собой гиперплоскость. Например, рассмотрим линейную модель двух переменных следующего вида:

W = –2x₁ –3x₂ (2.2)

при следующих ограничениях

x₁ – 4x₂ £ 4;

–2x₁ + x₂ £ 2;

х₁ ³ 0; x₂ ³ 0.

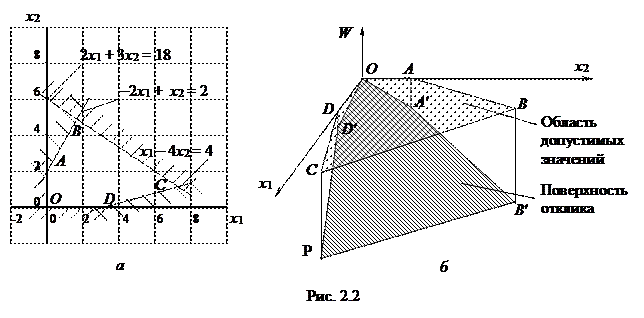
Область допустимых значений (область определения) OABCD для модели (2.2) образована ограничениями (2.3) (Рис. 2.2). Поверхность отклика представляет собой плоский многоугольник OA'B'C'D' (рис. 2.2, б).

При определенном соотношении ограничений множество допустимых решений может отсутствовать (пусто). Пример такого множества показан на рис. 2.3. Прямые АС и ВС ограничивают область допустимых значений сверху. Третье ограничение отсекает область допустимых значений снизу от прямой АВ. Таким образом, общей области, удовлетворяющей всем трем ограничениям, нет.

Линейные модели достаточно просты и поэтому, с одной стороны, предполагают существенное упрощение задачи, а с другой – допускают разработку простых и эффективных методов решения.

При исследовании ДЛА линейные модели используются редко и почти исключительно при приближенном описании задач.

Линейные модели могут использоваться при поэтапной аппроксимации нелинейных моделей (линеаризация задачи). Особенно эффективен этот прием при изучении небольших областей исследуемого пространства. Представление отдельных участков нелинейной поверхности отклика линейной моделью лежит в основе большой группы методов оптимизации, так называемых методов с линейной тактикой.

Исследование линейных моделей не представляет труда. В частности влияние каждой из переменных на характеристики модели вида

W = a₀ + a₁x₁ + a₂x₂ + …+ a_kx_k

задается ее коэффициентами:

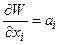, i = 1,…, k.

Для нахождения оптимума линейной модели W_опт разработан эффективный симплекс-метод.

К линейным иногда сводятся простейшие модели стоимости, рассматриваемые как совокупность производимых затрат.

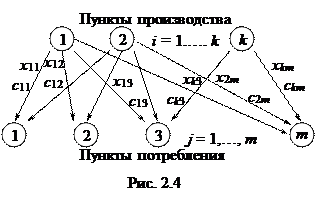Примером такой модели является классическая модель стоимости перевозок (транспортная задача) (Рис. 2.4).

Имеется k пунктов производства
(i = 1,…, k) и m пунктов потребления
(j = 1,…, m) некоторого продукта. Количество продукта, произведенного в каждом из k пунктов производства, равно a_i; количество продукта, необходимого в каждом из m пунктов потребления, равно b_j.

Предполагается равенство общего производства и потребления:

.

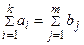Количество продукта, перевозимого из i-го пункта производства в j-й пункт потребления, равно x_ij; стоимость перевозки единицы этого продукта – с_ij.

Суммарная стоимость перевозок С_S задается линейной моделью:

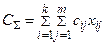
при следующих ограничениях

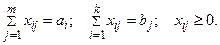
К линейным также относятся модели в виде линейных дифференциальных уравнений (обыкновенных или в частных производных).

Линейное обыкновенное дифференциальное уравнение n-го порядка имеет вид

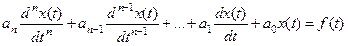. (2.10)

Начальные условия записываются как

.

Линейное дифференциальное уравнение в частных производных имеет вид

.

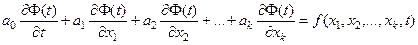Модель, заданная в виде дифференциального уравнения в частных производных, включает начальные и граничные условия (условия на границе области определения функции F(t)).