Метод максимального правдоподобия
Пусть 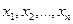 - выборка, полученная в результате проведения n независимых наблюдений за случайной величиной X. И пусть вид закона распределения величины X, например, вид плотности
- выборка, полученная в результате проведения n независимых наблюдений за случайной величиной X. И пусть вид закона распределения величины X, например, вид плотности 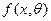 , известен, но неизвестен параметр
, известен, но неизвестен параметр  , которым определяется этот закон. Требуется по выборке оценить параметр
, которым определяется этот закон. Требуется по выборке оценить параметр  .
.
В основе метода максимального правдоподобия, предложенного Р. Фишером, лежит понятие функции правдоподобия.
Функцией правдоподобия, построенной на выборке 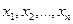 , называется функция аргумента
, называется функция аргумента  вида
вида
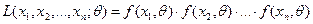
или
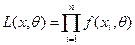 ,
,
где 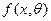 - плотность распределения случайной величины X в случае, если X - непрерывная. Если X - дискретная случайная величина, то функция правдоподобия имеет вид
- плотность распределения случайной величины X в случае, если X - непрерывная. Если X - дискретная случайная величина, то функция правдоподобия имеет вид
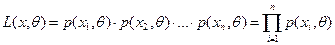
где 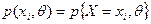 .
.
Из определения следует, что чем больше значение функции 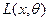 , тем более вероятно (правдоподобнее), при фиксированном
, тем более вероятно (правдоподобнее), при фиксированном  , появление в результате наблюдений чисел
, появление в результате наблюдений чисел 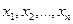 .
.
За точечную оценку параметра  , согласно методу максимального правдоподобия, берут такое его значение
, согласно методу максимального правдоподобия, берут такое его значение  , при котором функция правдоподобия достигает максимума.
, при котором функция правдоподобия достигает максимума.
Эта оценка, называемая оценкой максимального правдоподобия, является решением уравнения

Так как функции 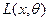 и
и 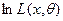 достигают максимума при одном и том же значении
достигают максимума при одном и том же значении  , то вместо отыскания максимума функции
, то вместо отыскания максимума функции 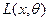 ищут максимум функции
ищут максимум функции 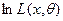 .
.
Таким образом, для нахождения оценки максимального правдоподобия надо:
1. Решить уравнение правдоподобия
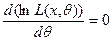 .
.
2. Отобрать то решение, которое обращает функцию 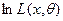 в максимум (удобно использовать вторую производную: если
в максимум (удобно использовать вторую производную: если
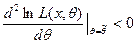
то 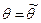 - точка максимума).
- точка максимума).
Если оценке подлежат несколько параметров 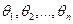 распределения, то оценки
распределения, то оценки  определяются решением системы уравнений правдоподобия:
определяются решением системы уравнений правдоподобия:
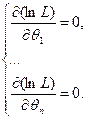
Пример 9.3. Найти оценку параметра а распределения Пуассона методом максимального правдоподобия.
Решение:
В данном случае 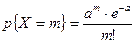 . Поэтому
. Поэтому
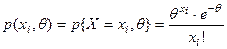
При 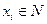 , составляем функцию правдоподобия (для дискретной случайной величины Х)
, составляем функцию правдоподобия (для дискретной случайной величины Х)
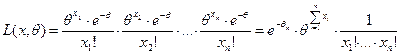
Тогда
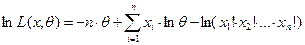
и
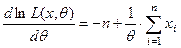 .
.
Уравнение правдоподобия имеет вид:
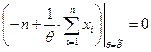 .
.
Отсюда находим
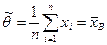 .
.
А так как
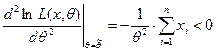 ,
,
то оценка 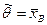 является оценкой максимального правдоподобия. Итак
является оценкой максимального правдоподобия. Итак 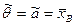 .
.
Дата добавления: 2017-03-29; просмотров: 748;
