Доверительный интервал для математического ожидания при известной дисперсии

Пусть случайная величина 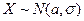; σ - известна и доверительная вероятность (надежность) 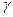- задана.

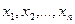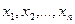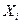Пусть - выборка, полученная в результате проведения n независимых наблюдений за случайной величиной X. Чтобы подчеркнуть случайный характер величин , перепишем их в виде , т.е. под будем понимать значение случайной величины X в i-м опыте. Случайные величины - независимы, закон распределения любой из них совпадает с законом распределения случайной величины X (т.е. ). А это значит, что

,

.

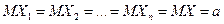Выборочное среднее

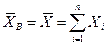
также будет распределено по нормальному закону (примем без доказательства). Параметры распределения 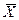таковы: , .

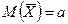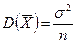Действительно,

^,

^.

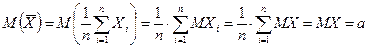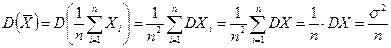Таким образом, .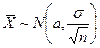

Следовательно, пользуясь формулой

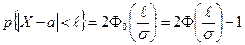
можно записать

_,

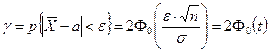где 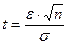. Из последнего равенства находим

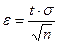, (9.3)

поэтому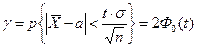

или

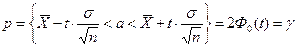. (9.4)

В соответствии с определением доверительного интервала получаем, что доверительный интервал для 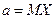есть

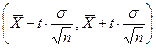, (9.5)

где t определяется из равенства (9.4), т.е. из уравнения

(9.6)

или

).

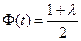При заданном 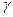по таблице функции Лапласа находим аргумент t.

Заметим, что из равенства (9.3) следует: с возрастанием объема выборки n число ε убывает и, значит, точность оценки увеличивается. Увеличение надежности 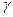влечет уменьшение точности оценки.

Пример 9.5. Произведено 5 независимых наблюдений над случайной величиной 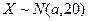. Результаты наблюдений таковы: 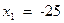, , 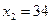, , 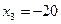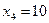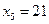. Найти оценку для 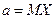, а также построить для него 95%-й доверительный интервал.

Решение:

Находим сначала :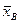

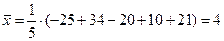, т.е. .

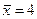Учитывая, что 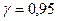и 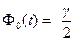, получаем .

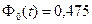По таблице выясняем, что .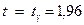

Тогда .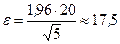

Согласно (9.6) доверительный интервал для 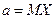таков:

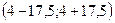, т.е. (-13,5; 21,5).