Доверительный интервал для среднего квадратического отклонения нормального распределения
Пусть случайная величина 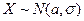 , где σ - неизвестно,
, где σ - неизвестно, 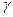 - задано. Можно показать, что если
- задано. Можно показать, что если 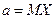 известно, то доверительный интервал для среднего квадратического отклонения σ имеет вид:
известно, то доверительный интервал для среднего квадратического отклонения σ имеет вид:
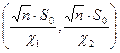 ,
,
где n - объем выборки, 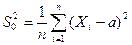 ,
,
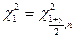 ,
, 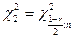
являются квантилями 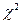 - распределения с n степенями свободы, определяемые по таблице квантилей
- распределения с n степенями свободы, определяемые по таблице квантилей 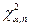 распределения
распределения 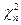 .
.
Если 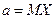 неизвестно, то доверительный интервал для неизвестного
неизвестно, то доверительный интервал для неизвестного 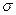 имеет вид:
имеет вид:
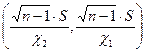 ,
,
где n - объем выборки, S2 = 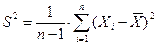 - исправленное среднее квадратическое отклонение, квантили
- исправленное среднее квадратическое отклонение, квантили

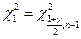 ,
, 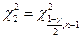
определяются по таблице 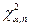 при
при 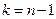 ,
, 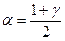 и
и 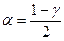 соответственно.
соответственно.
Скажем несколько слов о доверительном интервале для оценки вероятности успеха при большом числе испытаний Бернулли.
Доверительный интервал, который с надежностью 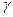 покрывает оцениваемый параметр р при больших значениях n (порядка сотен), имеет вид
покрывает оцениваемый параметр р при больших значениях n (порядка сотен), имеет вид 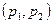 , где
, где
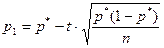 ,
, 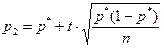 , (9.10)
, (9.10)
где 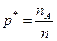 - относительная частота события A; t определяется из равенства
- относительная частота события A; t определяется из равенства 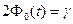 .
.
Для оценки приближенного равенства 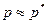 можно использовать равенство
можно использовать равенство
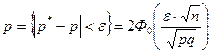 .
.
Пример 9.7. Для оценки параметра нормально распределенной случайной величины была сделана выборка объема в 30 единиц и вычислено 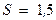 . Найти доверительный интервал, покрывающий а с вероятностью
. Найти доверительный интервал, покрывающий а с вероятностью 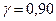 .
.
Решение:
Имеем 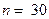 ,
, 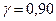 . По таблице
. По таблице 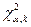 находим
находим
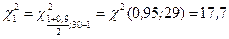
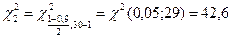
Доверительный интервал имеет вид
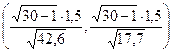 или
или 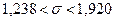 .
.
Дата добавления: 2017-03-29; просмотров: 383;
