Понятие интервального оценивания параметров
Точечные оценки неизвестного параметра  хороши в качестве первоначальных результатов обработки наблюдений. Их недостаток в том, что неизвестно, с какой точностью они дают оцениваемый параметр.
хороши в качестве первоначальных результатов обработки наблюдений. Их недостаток в том, что неизвестно, с какой точностью они дают оцениваемый параметр.
Для выборок небольшого объема вопрос о точности оценок очень существенен, так как между  и
и 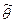 может быть большое расхождение в этом случае. Кроме того, при решении практических задач часто требуется определить и надежность этих оценок. Тогда и возникает задача о приближении параметра
может быть большое расхождение в этом случае. Кроме того, при решении практических задач часто требуется определить и надежность этих оценок. Тогда и возникает задача о приближении параметра  не одним числом, а целым интервалом
не одним числом, а целым интервалом  .
.
Оценка неизвестного параметра называется интервальной, если она определяется двумя числами - концами интервала.
Задачу интервального оценивания можно сфор£мулировать так: по данным выборки построить числовой интервал  , относительно которого с заранее выбранной вероятностью
, относительно которого с заранее выбранной вероятностью 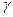 можно сказать, что внутри этого интервала находится точное значение оцениваемого параметра (рис. 9.1).
можно сказать, что внутри этого интервала находится точное значение оцениваемого параметра (рис. 9.1).

Рис. 9.1.
Интервал  , накрывающий с вероятностью
, накрывающий с вероятностью 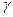 истинное значение параметра
истинное значение параметра  , называется доверительным интервалом, а вероятность
, называется доверительным интервалом, а вероятность 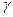 - надежностью оценки или доверительной вероятностью.
- надежностью оценки или доверительной вероятностью.
Очень часто доверительный интервал выбирается симметричным относительно несмещенной точечной оценки 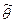 , т.е. выбирается интервал вида
, т.е. выбирается интервал вида 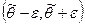 такой, что
такой, что
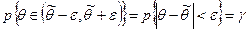
Число 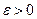 характеризует точность оценки: чем меньше разность
характеризует точность оценки: чем меньше разность 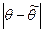 , тем точнее оценка.
, тем точнее оценка.
Величина 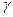 выбирается заранее, ее выбор зависит от конкретно решаемой задачи. Так, степень доверия авиапассажира к надежности самолета, очевидно, должна быть выше степени доверия покупателя к надежности телевизора, лампочки, игрушки... Надежность
выбирается заранее, ее выбор зависит от конкретно решаемой задачи. Так, степень доверия авиапассажира к надежности самолета, очевидно, должна быть выше степени доверия покупателя к надежности телевизора, лампочки, игрушки... Надежность 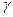 принято выбирать равной 0,9; 0,95; 0,99 или 0,999. Тогда практически достоверно нахождение параметра
принято выбирать равной 0,9; 0,95; 0,99 или 0,999. Тогда практически достоверно нахождение параметра  в доверительном интервале
в доверительном интервале 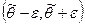 .
.
Дата добавления: 2017-03-29; просмотров: 383;
