Методы нахождения точечных оценок
Рассмотрим наиболее распространенные методы получения точечных оценок параметров распределения: метод моментов, метод максимального правдоподобия и метод наименьших квадратов.
Метод моментов
Метод моментов для нахождения точечных оценок неизвестных параметров заданного распределения состоит в приравнивании теоретических моментов распределения соответствующим эмпирическим моментам, найденных по выборке.
Так, если распределение зависит от одного параметра  (например, задан вид плотности распределения
(например, задан вид плотности распределения 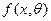 ), то для нахождения его оценки надо решить относительно
), то для нахождения его оценки надо решить относительно  одно уравнение:
одно уравнение:
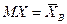
 - есть функция от
- есть функция от  .
.
Если распределение зависит от двух параметров (например, вид плотности распределения 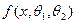 ) - надо решить относительно
) - надо решить относительно 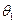 и
и 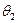 систему уравнений:
систему уравнений:

И, наконец, если надо оценить n параметров 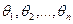 - надо решить одну из систем вида:
- надо решить одну из систем вида:
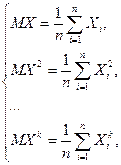 или
или 
Метод моментов является наиболее простым методом оценки параметров. Он был предложен в 1894 г. Пирсоном. Оценки метода моментов обычно состоятельны, однако их эффективность часто значительно меньше единицы.
Пример 9.2. Найти оценки параметров нормального распределения случайной величины X методом моментов.
Решение:
Требуется по выборке 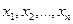 найти точечные оценки неизвестных параметров
найти точечные оценки неизвестных параметров 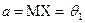 и
и 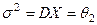 .
.
По методу моментов приравниваем их, соответственно, к выборочному среднему и выборочной дисперсии ( 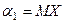 - начальный момент I порядка,
- начальный момент I порядка, 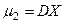 - центральный момент II порядка). Получаем
- центральный момент II порядка). Получаем
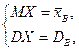 т.е.
т.е. 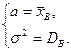
Итак, искомые оценки параметров нормального распределения:
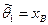 и
и 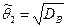 .
.
Дата добавления: 2017-03-29; просмотров: 720;
