Свойства статистических оценок

Качество оценки определяют, проверяя, обладает ли она свойствами несмещенности, состоятельности, эффективности.

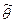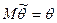Оценка параметра называется несмещенной, если . Если 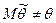, то оценка 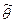называется смещенной.

Чтобы оценка 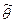не давала систематической ошибки (ошибки одного знака) в сторону завышения ( 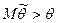) или занижения ( 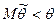), надо потребовать, чтобы математическое ожидание оценки было равно оцениваемому параметру.

Если 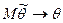, то оценка 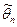называется асимптотически несмещенной.

Требование несмещенности особенно важно при малом числе наблюдений (опытов).

Оценка 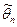параметра называется состоятельной, если она сходится по вероятности к оцениваемому параметру:

,

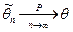т.е. для любого 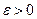выполнено

.

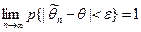Это означает, что с увеличением объема выборки мы все ближе приближаемся к истинному значению параметра , т.е. практически достоверно .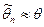

Свойство состоятельности обязательно для любого правила оценивания (несостоятельные оценки не используются).

Состоятельность оценки 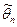может быть установлена с помощью следующей теоремы.

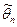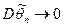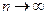Теорема 9.1. Если оценка параметра является несмещенной и при , то 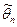- состоятельная оценка.

Доказательство. Запишем неравенство Чебышева для случайной величины 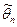для любого :

.

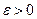Так как по условию 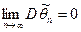, то 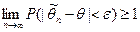. Но вероятность любого события не превышает 1 и, следовательно,

,

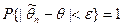т. е. 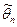- состоятельная оценка параметра .

Несмещенная оценка 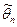параметра называетсяэффективной, если она имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра , т.е. оценка 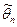эффективна, если ее дисперсия минимальна.

Эффективную оценку в ряде случаев можно найти, используя неравенство Рао-Крамера:

,

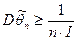где 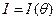- информация Фишера, определяющаяся формулой

- для дискретных величин:

,

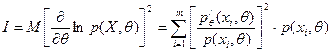где ,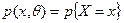

- для непрерывных величин:

,

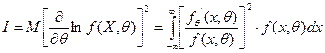где 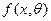- плотность распределения непрерывной случайной величины X.

Эффективность оценки определяется отношением

,

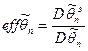где 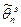— эффективная оценка. Чем ближе 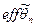к 1, тем эффективнее оценка 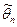. Есл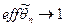и при 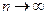, то оценка называется асимптотически эффективной.

Отметим, что на практике не всегда удается удовлетворить всем перечисленным выше требованиям (несмещенность, состоятельность, эффективность), и поэтому приходится довольствоваться оценками, не обладающими сразу всеми тремя свойствами. Все же три свойства, как правило, выделяют оценку однозначно.