Понятие оценки параметров

Оценки неизвестных параметров

Пусть изучается случайная величина X с законом распределения, зависящим от одного или нескольких параметров. Например, это параметр а в распределении Пуассона 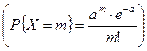или параметры а и σ для нормального закона распределения.

Требуется по выборке , полученной в результате n наблюдений (опытов), оценить неизвестный параметр .

Напомним, что - случайные величины: Х₁ - результат первого наблюдения, X₂ - второго и т.д., причем случайные величины 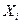, , 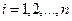имеют такое же распределение, что и случайная величина X. Конкретная выборка 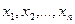- это значения (реализация) независимых случайных величин .

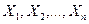Статистической оценкой 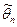(просто оценкой 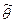) параметра теоретического распределения называют его приближенное значение, зависящее от данных выбора.

Очевидно, что оценка 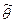есть значение некоторой функции результатов наблюдений над случайной величиной, т.е.

.

(9.1)

Функцию результатов наблюдений (т.е. функцию выборки) называют статистикой.

Можно сказать, что оценка 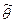параметра есть статистика, которая в определенном смысле близка к истинному значению .

Так, 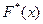есть оценка 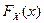, гистограмма - плотности .

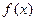Оценка 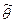является случайной величиной, так как является функцией независимых случайных величин 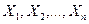. Если произвести другую выборку, то функция примет другое значение.

Если число опытов (наблюдений) невелико, то замена неизвестного параметра его оценкой 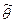, например математического ожидания средним арифметическим, приводит к ошибке. Это ошибка в среднем тем больше, чем меньше число опытов.

К оценке любого параметра предъявляется ряд требований, которым она должна удовлетворять, чтобы быть «близкой» к истинному значению параметра, т.е. быть в каком-то смысле «доброкачественной» оценкой.