Доверительный интервал для математического ожидания при неизвестной дисперсии

Пусть случайная величина 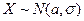, где σ - неизвестна, 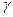- задана. Найдем такое число ε, чтобы выполнялось соотношение 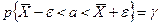или

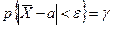. (9.7)

Введем случайную величину

,

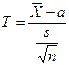где S - исправленное среднее квадратическое отклонение случайной величины X, вычисленное по выборке:

.

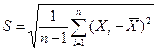Доказывается, что случайная величина Т имеет распределение Стьюдента с n-1 степенью свободы. Плотность этого распределения имеет вид:

,

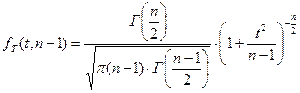где 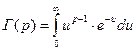- гамма-функция; 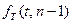- четная функция.

Перейдем в левой части равенства (9.7) от случайной величины 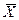к случайной величине Т: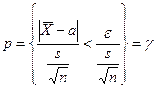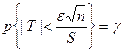

или или , где

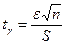. (9.8)

Величина 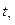находится из условия

,

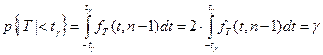т.е. из равенства

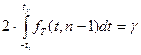
Пользуясь таблицей квантилей распределения Стьюдента, находим значение 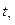в зависимости от доверительной вероятности 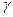и числа степеней свободы n-1 ( 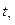- квантиль уровня ) .

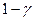Определив значение 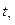из равенства (9.8), находим значение ε:

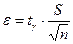. (9.9)

Следовательно, равенство (9.7) принимает вид

.

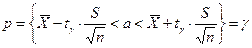А это значит, что интервал

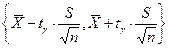
покрывает 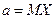с вероятностью 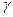, т.е. является доверительным интервалом для неизвестного математического ожидания случайной величины X.

Пример 9.6.По условию задачи 9.5, считая, что случайная величина 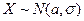, построить для неизвестного 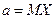доверительный интервал. Считать .

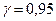Решение:

Оценку 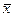для MX уже знаем: 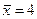. Находим значение S:

,

.

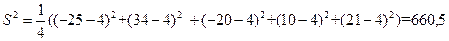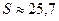По таблице для 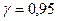и 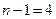находим .

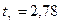Следовательно, .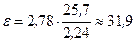

Доверительный интервал таков (-27,9; 35,9).