Результаты расчета разностей по столбцам

В	А
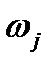
А1	А2	А3
В1 В2 В3 В4	0,1225 0,3925 -0,0775 -0,4375	-0,3075 -0,1775 0,2925 0,1925	-0,623 0,307 -0,093 0,407	0,7455 0,5700 0,3700 0,8445

- Для каждого j значения 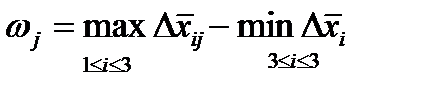приведены в последнем столбце таблицы 4.13.

- Далее находим:

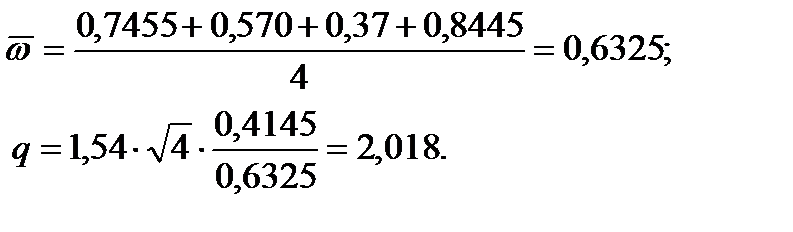
Из таблицы 123 [12] для m=4 (входим в таблицу с n=3) и f=5,4 (используем интерполяцию), при α=0,95 находим q_0,95(4; 5,4)=5,2.

Так как q=2,018 < q_0,95(4; 5,4)=5,2 - этот критерий не выявил влияние факторов А и В на наблюдаемый процесс. К сожалению, выделить влияние взаимодействия факторов А и В с помощью этого критерия невозможно.

4.2. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ НОРМАЛЬНО РАСПРЕДЕЛЕННЫХ СЛУЧАЙНЫХ ВЕЛИЧИН [12, 14]

Корреляционный анализ предполагает изучение зависимости между случайными величинами с одновременной количественной оценкой степени не случайности их совместного изменения.

Изменение случайной величины y, соответствущее изменению случайной величины х, разбивается на две составляющие – стохастическую, связанную с неслучайной зависимостью у от х, и случайную (или статистическую), связанную со случайным характером поведения самих у и х.

Статистическая составляющая связи между у и х характеризуется коэффициентом корреляции.

Коэффициент корреляции показывает, насколько связь между случайными величинами близка к строго линейной. Если у и х распределены нормально, равенство ρ=0 указывает на отсутствие линейной связи между ними. Значение ρ=±1 соответствует строго линейной связи между у и х (знак указывает на направление связи).

Однако коэффициент корреляции ρ не учитывает возможной криволинейной связи между случайными величинами. Для учета таких связей используется корреляционное отношение, введенное К. Пирсоном.

Если у и х связаны строго линейно, то Ƞ²=ρ²=1. Если между х и у существует линейная стохастическая связь, то Ƞ²=ρ²<1. При нелинейной стохастической связи ρ²<Ƞ²<1. В любом случае имеет место неравенство 0≤ρ²≤Ƞ²≤1 (равенство достигается толь при строгой линейной связи между у и х).