Результаты исследования

В	А
А1	А2	…	Аi	…	Аk
В1 В2 . . . Вj . . . Вm	x11 x12 … … … x1j … … … x1m	x21 x22 … … … x2j … … … x2m	… … … … … … … … … …	xi1 xi2 … … … xij … … … xim	… … … … … … … … … …	xk1 xk2 … … … xkj … … … xkm	X1’ X2’ … … … Xj’ … … … Xm’
	X1	X2	…	Xi	…	Xk

Дисперсионный анализ для двухфакторных таблиц проводится в следующей последовательности:

- Вычисляются суммы:

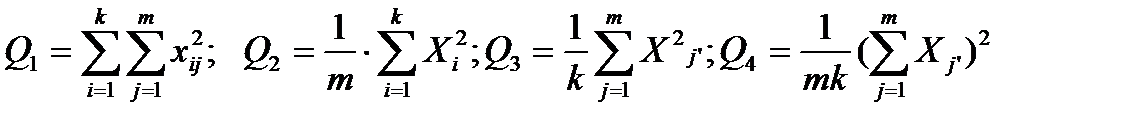(4.29)

- Далее находятся оценки дисперсий:

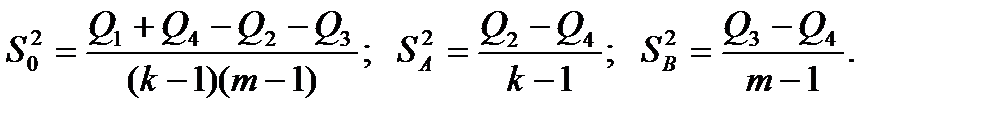(4.30)

Если:

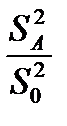> F_α(f₁;f₂), (4.31)

где f₁=k-1 и f₂=(k-1)*(m-1), то влияние фактора А с достоверностью α признается значимым.

Аналогично значимым признается влияние факторов В (f₁=m-1 и f₂=(k-1)*(m-1)).

Приведенный анализ предполагает независимость факторов А и В. Если они зависимы, то взаимодействие факторов С=А*В также является фактором, которому соответствует своя дисперсия. Для того, чтобы выделить такое взаимодействие, необходимы параллельные наблюдения в каждой клетке таблицы, т.е. при каждом сочетании факторов А и В на уровнях A_i и B_i соответственно необходимо не одно наблюдение, а серия наблюдений x_ij1, x_ij2,…, x_ijn. Пусть x_ij теперь является средним из n наблюдений, т.е.:

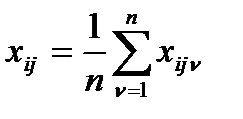. (4.32)

Для оценки влияния взаимодействия факторов А*В вычисляем дополнительную сумму:

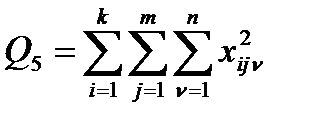. (4.33)

Далее анализ производится, как и ранее, с той лишь разницей, что в клетках таблицы вместо отдельных значений 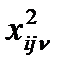, используются их средние значения (4.32) .

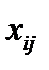- Вычисляется дисперсия:

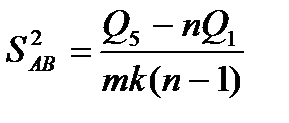(4.34)

- Проверяется значимость взаимодействия факторов А*В критерием:

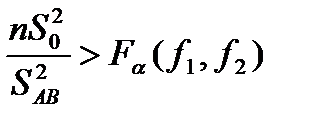, (4.35)

где f₁=(k-1)*(m-1) и f₂=m*k*(n-1).

С добавлением каждого нового фактора принципиальная основа дисперсионного анализа не изменяется, но существенно усложняются формулы и таблицы для расчетов. Подробное изложение прикладных методов дисперсионного анализа для случая трех, четырех и более факторов с анализом различных практических ситуаций содержится в [13].

Пример [12]: Провести двухфакторный дисперсионный анализ данных, представленных в таблице 4.8, при доверительной вероятности α=0,95.

Таблица 4.8