ДИСПЕРСИОННЫЙ АНАЛИЗ С ИСПОЛЬЗОВАНИЕМ РАЗМАХОВ
Рассмотрим схему двухфакторного дисперсионного анализа с k уровнями фактора A и m уровнями фактора В (при каждом сочетании уровней факторов одно наблюдение или среднее из нескольких наблюдений). Для выявления значимости влияния изучаемых факторов можно использовать следующее выражение:
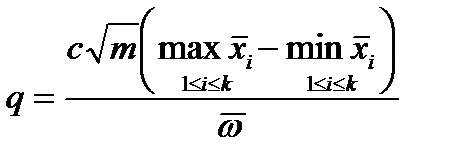. (4.36)
Критические точки для статистики q приведены в [12, таблица 123] для различных m (в таблице 123 вместо n следует использовать m) и f. Количество эквивалентных степеней свободы f для нашего случая и значение коэффициента с приведены в таблице 4.10.
Средний размах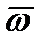 
вычисляется следующим образом:
- Для каждого уровня Аi находим:
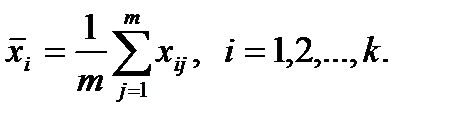(4.37)
- Затем для всех уровней фактора В при i-м уровне фактора А вычисляем m разностей:
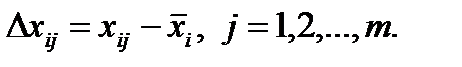(4.38)
- Далее находим:
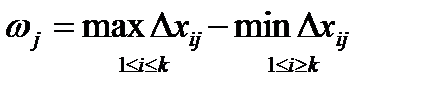(4.39)
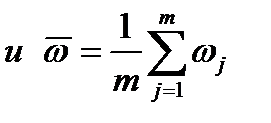(4.40)
Таблица 4.10
Масштабный коэффициент “c” и эффективное число степеней свободы “f” для двухфакторного дисперсионного анализа
| m | k | |||||||
| f | c | f | c | f | c | f | c | |
| 1,00 1,90 2,70 3,60 4,50 5,40 6,30 7,10 8,10 16,70 | 1,00 1,05 1,07 1,08 1,09 1,09 1,10 1,10 1,10 11,10 | 2,00 3,70 5,40 7,20 8,90 10,70 12,50 14,30 16,10 33,90 | 1,35 1,48 1,54 1,57 1,59 1,61 1,62 1,63 1,63 1,66 | 2,90 5,60 8,20 10,90 13,60 16,30 19,00 21,70 24,40 51,50 | 1,58 1,76 1,84 1,88 1,91 1,93 1,95 1,96 1,97 2,02 | 3,80 7,40 11,00 14,60 18,20 21,80 25,40 29,00 32,60 68,80 | 1,75 1,96 2,06 2,12 2,15 2,18 2,20 2,21 2,22 2,28 |
Превышение выборочной статистикой q ее критического значения qα(m.f) (из таблицы 123 [12]) приводит к признанию значимости влияния изучаемых факторов.
Пример: Провести дисперсионный анализ в условиях примера по п.4.1.2 с помощью размахов. Исходные данные представлены в таблице 4.11.
Таблица 4.11
Исходные данные
| В | А | ||
| А1 | А2 | А3 | |
| В1 В2 В3 В4 | 3,83 4,10 3,63 3,27 | 3,00 3,13 3,60 3,50 | 2,67 3,60 3,20 3,70 |
Имеем k=3, m=4. Из таблицы 4.10 для k=3, m=4 находим c=1,54 и f=5,4.
- Далее находим средние по столбцам (уровни фактора А):
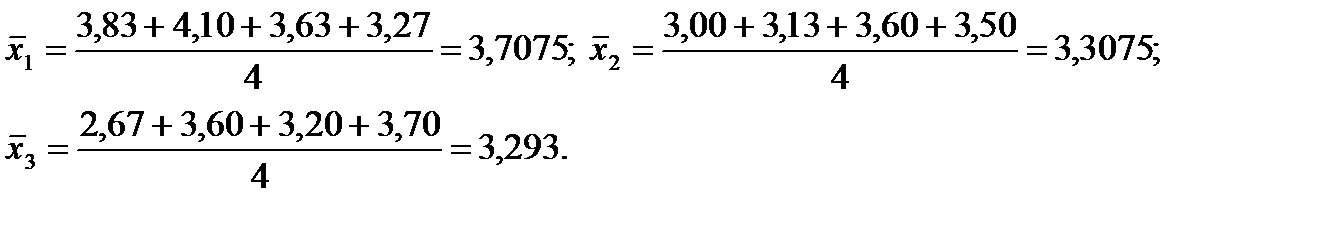
Следовательно:
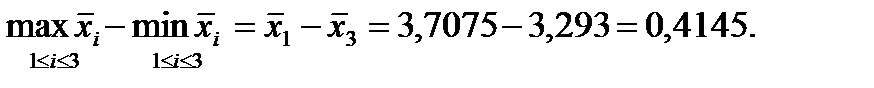
- Теперь вычислим m=4 разностей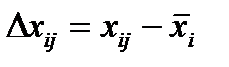 
для всех i=1,2,…,m.
Результаты сведены в таблицу 4.12.
Таблица 4.12
Дата добавления: 2018-11-25; просмотров: 245;