Экспериментальные данные

Номер наблюдения	Уровни фактора А
А1 А2 … Аi … Аk
. j . n	x11 x21 … xi1 … xk1 x12 x22 … xi2 … xk2 . .. .… . .. … …. … x1j x2j… … x i j … x k j . . … . .. … … … x1n x2n … … xi n …. x k n
	X1 X2 … Xi … Xk

Рассмотрим оценки различных дисперсий, возникающие при анализе таблицы результатов наблюдений. Для дисперсии, характеризующей изменение данных на уровне A_i (по строкам таблицы), имеем:

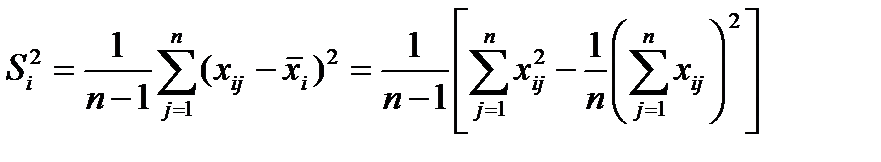. (4.14)

Из предпосылок дисперсионного анализа следует, что должно иметь место равенство 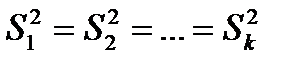, что проверяется соответствующим критерием сравнения.

При выполнении условия 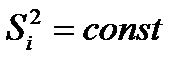(при i=1,2,…k) находим оценку дисперсии, характеризующей рассеяние значений x_ij вне влияния фактора А, по формуле:

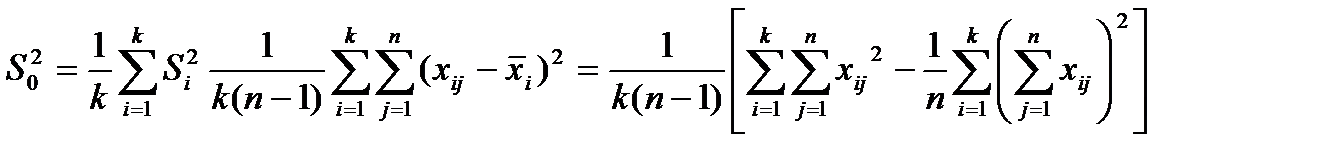. (4.15)

Оценка 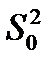имеет k*(n-1) степеней свободы.

Общая выборочная дисперсия всех наблюдений равна:

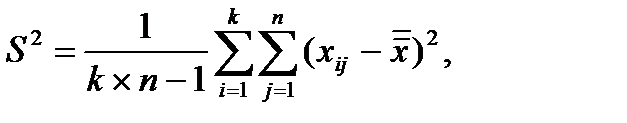(4.16)

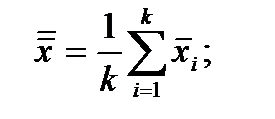(4.17)

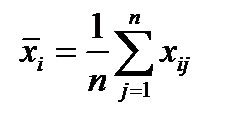(4.18)

Следовательно:

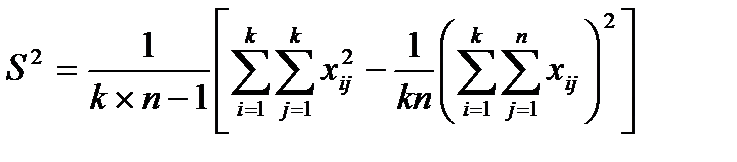. (4.19)

Введем теперь оценку дисперсии 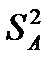, характеризующей изменение средних 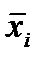, связанное с влиянием фактора А:

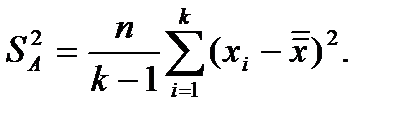(4.20)

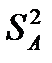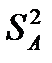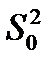Очевидно, что при оценке используется (k-1) степеней свободы. Теперь проверка влияния фактора А на изменение средних может быть сведена к сравнению дисперсий и . Влияние фактора А признается значимым, если значимо отношение 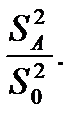Отношение 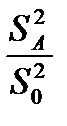признается значимым с вероятностью α, если:

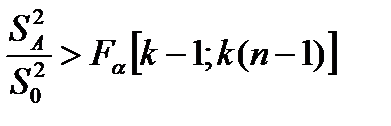, (4.21)

где 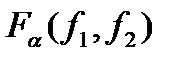- α- квантиль F- распределения с 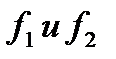степенями свободы.

Для нахождения 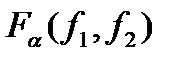могут быть использованы специальные таблицы, например, из [2].

Для упрощения вычислений приведем алгоритм их выполнения [12]:

- Вычисляем последовательно суммы:

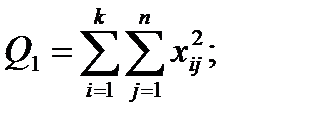(4.22)

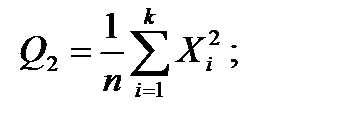(4.23)

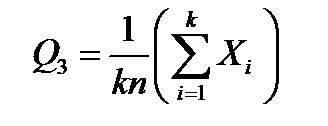(4.24)

- Далее находим:

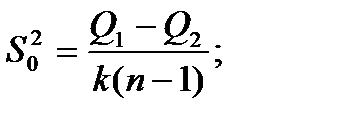(4.25)

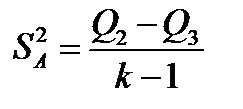(4.26)

Сравнением 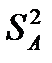и 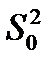, устанавливаем наличие влияние фактора А.

Если:

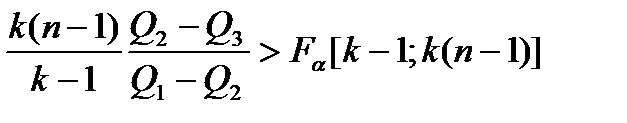, (4.27)

то влияние фактора А признается значимым. В ином случае всю выборку наблюдений можно считать однородной с общей дисперсией:

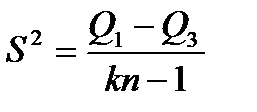. (4.28)

Пример: Провести дисперсионный анализ данных, представленных в таблице 4.6, при доверительной вероятности α=0,95.

Таблица 4.6