ДИСПЕРСИОННЫЙ АНАЛИЗ НОРМАЛЬНО РАСПРЕДЕЛЕННЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
Дисперсионный анализ является статистическим методом анализа результатов наблюдений, зависящих от различных одновременно действующих факторов, с целью выбора наиболее значимых факторов и оценки их влияния на исследуемый процесс.
Влияние различных факторов на изучаемые случайные величины (например, влияние режима нагрузки на долговечность технического изделия) приводит к изменению значений параметров распределения вероятностей этих величин – среднего, дисперсии или моментов более высокого порядка.
С помощью дисперсионного анализа устанавливаются изменения дисперсии результатов эксперимента при изменении уровней изучаемого фактора. Если дисперсии будут отличаться значимо, то следует вывод о значимом влиянии фактора на среднее значение наблюдаемой случайной величины.
Классические методы дисперсионного анализа основываются на следующих предпосылках: распределение исходных случайных величин нормально; дисперсии экспериментальных данных одинаковы для всех условий эксперимента (т.е. для экспериментов, выполненных на различных уровнях изучаемого фактора).
Поэтому, при проведении дисперсионного анализа следует предварительно проверить нормальность распределения изучаемой случайной величины и неразличимость дисперсий изучаемых совокупностей.
ПРОВЕРКА ГИПОТЕЗЫ О НОРМАЛЬНОМ РАСПРЕДЕЛЕНИИ СЛУЧАЙНОЙ ВЕЛИЧИНЫ ПРИ ПОМОЩИ МОДИФИЦИРОВАННОГО КРИТЕРИЯ Χ2 [9, 12]
С помощью данного критерия оцениваются параметры распределения по негруппированной выборке. После оценки параметров распределения совокупность выборочных данных разбивается на k равновероятных интервалов ( 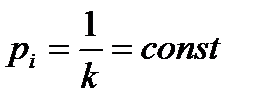 ) и статистика критерия подсчитывается по формуле:
) и статистика критерия подсчитывается по формуле:
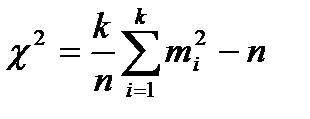 (4.1)
(4.1)
где n – объем выборки; mi – количество членов выборки, попавшее в i-й интервал.
Границы интервалов определяются следующим образом:
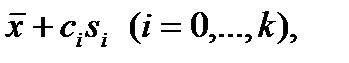 (4.2)
(4.2)
где 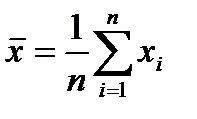 (4.3)
(4.3)
и 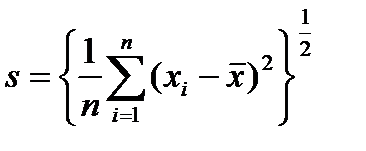 . (4.4)
. (4.4)
Значение коэффициентов ci приведены в таблице 4.1 [4]. Следует помнить, что с0=-∞ и сk=∞.
Таблица 4.1
Значения коэффициентов ci модифицированного χ2- критерия нормальности для k =3 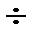 15
15
| k | c1 | c2 | c3 | c4 | c5 | c6 | c7 |
| -0,4307 -0,6745 -0,8416 -0,9674 -1,0676 -1,1503 -1,2206 -1,2816 -1,3352 -1,3830 -1,4261 -1,4652 -1,5011 | -0,2533 -0,4307 -0,5659 -0,6745 -0,7647 -0,8416 -0,9085 -0,9674 -1,0201 -1,0676 -1,1108 | -0,1800 -0,3186 -0,4307 -0,5244 -0,6046 -0,6745 -0,7363 -0,7916 -0,8416 | -0,1397 -0,2533 -0,3488 -0,4307 -0,5024 -0,5660 -0,6229 | -0,1142 -0,2194 -0,2934 -0,3661 -0,4307 | -0,0966 -0,1800 -0,2533 | -0,0837 |
Так как ci симметричны относительно нуля, то недостающие знаки ci можно найти из соотношений:
 для нечетных
для нечетных 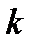 ; (4.5)
; (4.5)
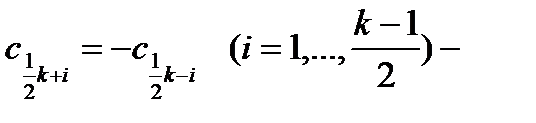 для четных
для четных 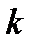 . (4.6)
. (4.6)
Если χ2 > dk(α), где dk(α) – критическое значение статистики критерия на уровне значимости α, то гипотеза нормальности отклоняется. Критические значения dk(α) приведены в таблице 4.2 [12].
Таблица4.2
Критическое значение dk(α) модифицированного χ2 – критерия нормальности
| k | α | k | α | ||||
| 0,10 | 0,05 | 0,01 | 0,10 | 0,05 | 0,01 | ||
| 2,371 3,928 5,442 6,905 8,322 9,703 11,055 | 3,248 5,107 6,844 8,479 10,038 11,543 13,007 | 5,418 7,917 10,075 12,021 13,837 15,567 17,234 | 12,384 13,694 14,988 16,267 17,535 18,792 | 14,438 15,843 17,226 19,589 19,937 21,270 | 18,852 20,431 21,977 23,495 24,990 26,464 |
Пример [12]:Имеется ряд выборочных значений случайной величины (n=100):
43 76 84 91 95 101 105 114 122 129
54 77 84 91 96 101 106 114 122 132
56 77 85 91 96 101 107 115 122 134
57 78 85 91 96 103 107 116 123 136
61 78 86 92 97 103 107 116 124 136
64 79 87 92 97 104 108 116 124 138
67 79 87 93 98 104 111 117 125 143
73 82 87 93 98 104 112 118 125 143
74 82 88 93 99 104 113 118 125 145
76 83 89 95 101 105 114 119 126 150
Необходимо проверить модифицированным критерием χ2 на уровне значимости α = 0,1 гипотезу нормальности распределения при оценке его параметров по негруппированным данным.
Имеем 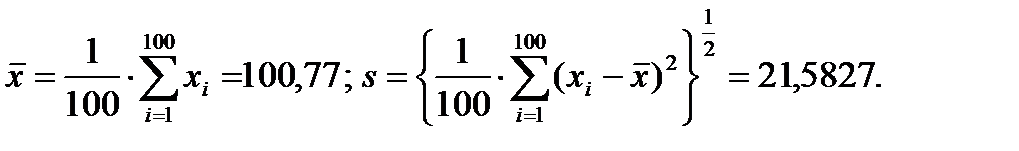
Из таблицы 4.1 находим коэффициенты разбиения (принимаем k=10): с1=-1,2816; с4=-0,2533; с7=0,5244; с2=0,8416; с5=0; с8=0,8416; с3=0,5244; с6=0,2533; с9=1,2816.
Результаты расчетов сведем в таблицу 4.3.
Таблица 4.3
Дата добавления: 2018-11-25; просмотров: 594;
