ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ УРАВНЕНИЯ РЕГРЕССИИ
Рассмотрим определение коэффициентов уравнения регрессии для трехфакторной модели [2, 10]:
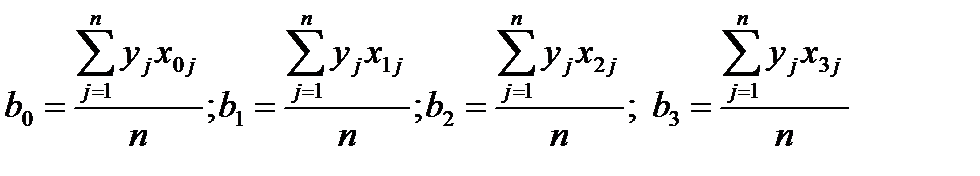 (3.13)
(3.13)
Следовательно, любые коэффициенты уравнения определяются скалярным произведением столбца y на соответствующий столбец Хi.
Можно показать, что аналогичным образом определяются коэффициенты, если в уравнении регрессии учитываются линейные взаимодействия (двойные, тройные и т.д.):
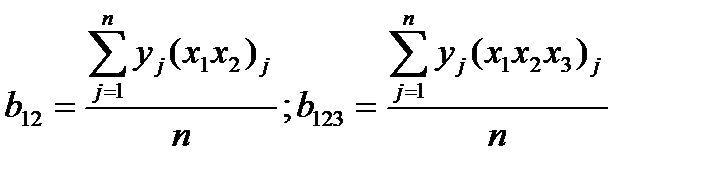 (3.14)
(3.14)
Следует обратить особое внимание на то, что все линейные коэффициенты независимы, так как в формулы для их расчета (3.13), (3.14) входят свои одноименные переменные. Поэтому каждый коэффициент характеризует роль соответствующей переменной в процессе или силу влияния фактора. Чем больше численная величина коэффициента, тем большее влияние оказывает этот фактор. Если коэффициент имеет знак плюс, то с увеличением значения фактора отклик увеличивается, а если минус - уменьшается.
В результате определения уравнения регрессии может получиться так, что один (или несколько) коэффициентов не очень большие и окажутся незначимыми. Факторы, имеющие коэффициенты, незначимо отличающиеся от нуля, могут быть выведены из состава уравнения, так как влияние на параметры отклика будет отнесено к ошибке эксперимента. Учитывая ортогональность плана, оставшиеся коэффициенты уравнения регрессии можно не пересчитывать. При отсутствии ортогональности плана эксперимента все коэффициенты необходимо пересчитывать заново.
Рассмотрим пример статистической обработки результатов полного двухфакторного эксперимента [2, 9, 10].
Таблица 3.2
План полного двухфакторного эксперимента
| Номер опыта | Факторы | Функция отклика | |||
| X0 | X1 | X2 | X1*X2 | ||
| + | - | - | + | Y1э | |
| + | + | - | - | Y2э | |
| + | - | + | - | Y3э | |
| + | + | + | + | Y4э |
Для полного двухфакторного эксперимента уравнение регрессии имеет вид:
Yт=b0+b1*X1+b2*X2+b12*X1*X2 (3.15)
По таблице 3.2 находим коэффициенты регрессии:
b0=y1э+y2э+y3э+y4э, (3.16)
b1=(-1)*y1э+(+1)*y2э+(-1)*y3э+(+1)*y4э, (3.17)
b2=(-1)*y1э+(-1)*y2э+(+1)*y3э+(+1)*y4э, (3.18)
b12=(+1)*y1э+(-1)*y2э+(-1)*y3э+(+1)*y4э. (3.19)
Значения коэффициентов указывают на силу влияния факторов на функцию цели. Некоторые из коэффициентов регрессии могут оказаться пренебрежимо малыми – незначимыми. Для установки факта незначимости коэффициента необходимо вычислить оценки дисперсии, с которой они определялись [2, 10, 11]:
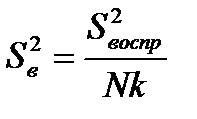 , (3.20)
, (3.20)
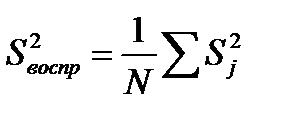 , (3.21)
, (3.21)
где k – число параллельных опытов.
Построчные (выборочные) дисперсии подсчитываются по формуле:
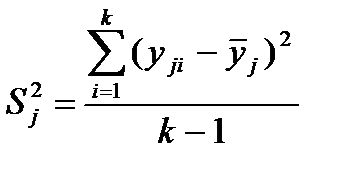 , (3.22)
, (3.22)
где 
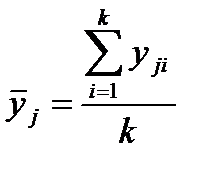 - средний отклик по k опытам в точке с номером j.
- средний отклик по k опытам в точке с номером j.
С оценками дисперсий 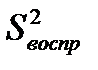 и
и 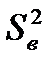 связывают число степеней свободы:
связывают число степеней свободы:
fвоспр=N(k-1). (3.23)
Принято считать, что коэффициент регрессии значим, если выполнено условие [2, 9, 10, 11]:
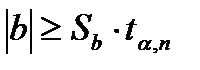 , (3.24)
, (3.24)
где 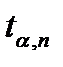 - значение критерия Стьюдента, которое находят по таблицам; индекс α – заданная доверительная вероятность;
- значение критерия Стьюдента, которое находят по таблицам; индекс α – заданная доверительная вероятность;
n= fвоспр=N(k-1).
В противном случае коэффициент незначим, и соответствующий член можно исключить из уравнения регрессии.
Далее следует проверить адекватность полученного уравнения регрессии.
Под адекватностью в данном случае понимают способность построенной математической модели соответствовать результатам эксперимента с заданной степенью точности. Эту проверку осуществляют с помощью критерия Фишера [2, 9 , 10, 11]:
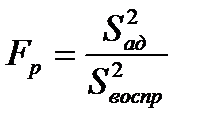 , (3.25)
, (3.25)
где 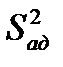 - оценка дисперсии адекватности.
- оценка дисперсии адекватности.
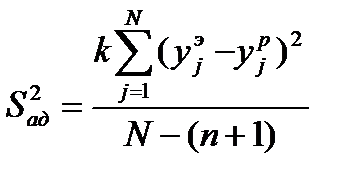 , где (3.26)
, где (3.26)
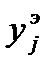 ,
, 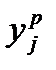 - экспериментальные и расчетные значения функции отклика в j–ом опыте; N–число опытов ПФЭ; n–число факторов; k–число параллельных опытов.
- экспериментальные и расчетные значения функции отклика в j–ом опыте; N–число опытов ПФЭ; n–число факторов; k–число параллельных опытов.
С дисперсией адекватности (3.26) связывают число степеней свободы:
fад=N-(n+1). (3.27)
По таблицам для критерия Фишера, зная fвоспр и fад определяют табличное значение FT. Уравнение регрессии считается адекватным, если выполняется условие:
Fp≤FT. (3.28)
Функция цели Yт найдена для кодированных факторов, далее можно перейти обратно к натуральным значениям данных факторов.
3.2.3. МЕТОД ДРОБНЫХ РЕПЛИК [2, 10]
Во многих практических задачах взаимодействия второго и высших порядков отсутствуют или пренебрежимо малы. Кроме того, на первых этапах исследования часто необходимо получать в первом приближении лишь линейную аппроксимацию изучаемого уравнения при минимальном числе экспериментов. Так, для трех факторов вместо уравнения (3.5) достаточно рассмотреть уравнение вида:
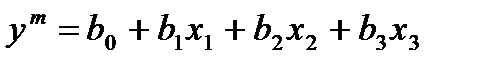 (3.29)
(3.29)
и определить только четыре коэффициента. Поэтому использование ПФЭ для определения коэффициентов только при линейных членах неэффективно из-за реализации большого числа опытов, особенно при большом числе факторов k. Если при решении задачи можно ограничиться линейным приближением, то в ПФЭ оказывается много «лишних» опытов. Так, для трех факторов достаточно 4 опыта, а в ПФЭ их 8.
Так, для определения коэффициентов уравнения (3.28) достаточно ограничится четырьмя опытами, если в ПФЭ 23 использовать х1х2 в качестве плана для х3, тогда матрица планирования эксперимента примет вид, представленный в таблице 3.3.
Таблица 3.3
Дата добавления: 2018-11-25; просмотров: 1212;
