ОЦЕНКА КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ
Рассматриваются нормально распределенные случайные величины у и х – (х1,у1), (х2,у2),…,(хi,уi),…,(хn,уn). Выборочной оценкой коэффициента корреляции ρ является случайная величина:
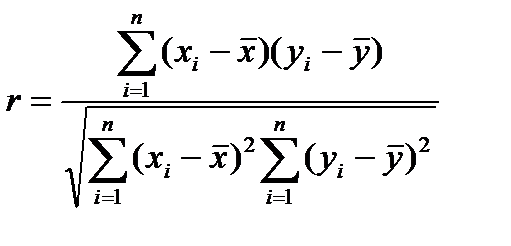, (4.41)
где 
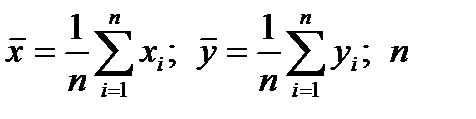- объем выборки.
При малых значениях n (n<15) лучшей оценкой коэффициента корреляции является:
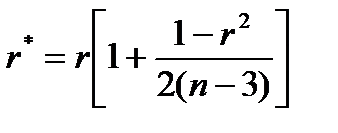(4.42)
На практике наибольший интерес представляет задача проверки гипотезы о значимости корреляционной связи между случайными величинами, т.е. значимости отклонения коэффициента корреляции ρ от нуля. В принятых обозначениях проверяется нулевая гипотеза Н0: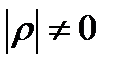 
.
Эта гипотеза проверяется сравнением выборочного значения коэффициента корреляции r с его критическим значением rα, являющимся α – квантилью распределения r при ρ=0. Корреляция между случайными величинами признается значимой, если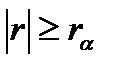 
. Критические значения rα приведены в таблице 4.13.
Ниже представлены формулы для оценки критического значения rα:
- при n>5
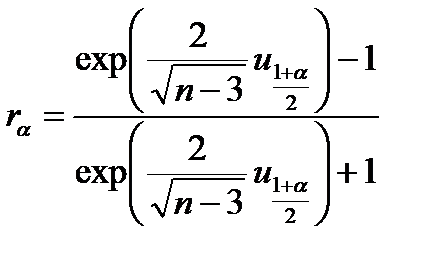; (4.43)
- при n>10
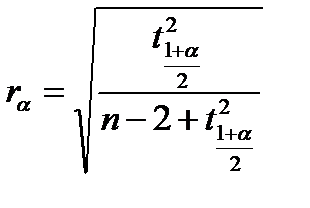; (4.44)
при n>200
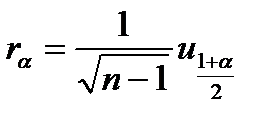. (4.45)
Здесь uα и tα – α-квантили соответственно стандартного нормального распределения и распределения Стьюдента с f=n-2 степенями свободы.
Таблица 4.13
Критические значения rα выборочного коэффициента корреляции для ρ=0 [12]
| n | доверительная вероятность α | n | доверительная вероятность α | ||||
| 0,90 | 0,95 | 0,99 | 0,90 | 0,95 | 0,99 | ||
| 0,988 0,900 0,805 0,729 0,669 0,621 0,582 0,549 0,521 0,497 | 0,997 0,950 0,878 0,811 0,754 0,707 0,666 0,632 0,602 0,576 | 1,000 0,990 0,959 0,917 0,874 0,834 0,798 0,765 0,735 0,708 | 0,476 0,457 0,441 0,426 0,412 0,400 0,389 0,378 0,369 0,360 | 0,553 0,532 0,514 0,497 0,482 0,468 0,456 0,444 0,433 0,423 | 0,684 0,661 0,641 0,623 0,606 0,590 0,575 0,561 0,549 0,537 |
Если гипотеза о значимости корреляции между случайными величинами не отклоняется, значит между случайными величинами x и y наблюдается связь.
Пример [4]: в результате наблюдений над случайными величинами х и у получена следующая совокупность данных при (n=10):
x: 2 4 1 7 3 11 14 15 21 4
y: 7 6 4 11 2 21 31 23 40 15
Необходимо проверить гипотезу о наличии корреляции между случайными величинами х и у с достоверностью α=0,95.
Находим:
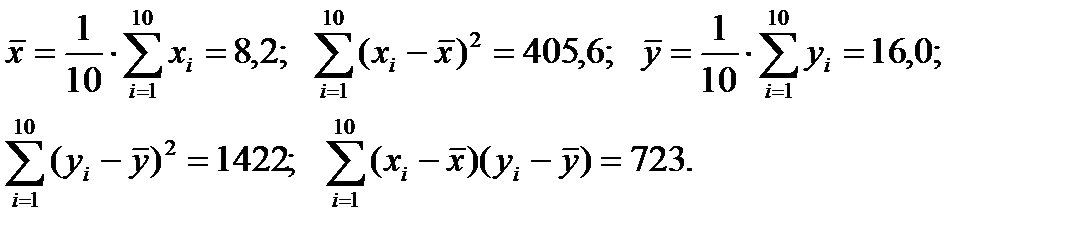
Далее получаем оценки коэффициента корреляции:
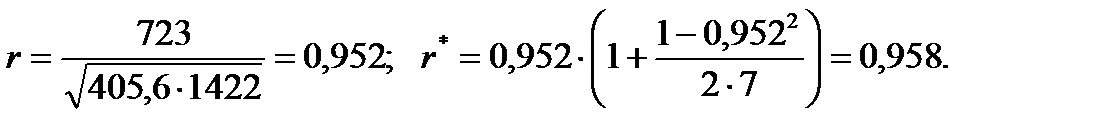
Из таблицы 4.13 для n=10 и r0,95=0,632.
Так как r(r*)=0,952(0,958)>r0,95=0,632, наличие зависимости между величинами х и у следует признать значимой с достоверностью α=0,95.
Если воспользоваться уравнениями 4.43 - 4.45 для расчета rα (имея в виду, что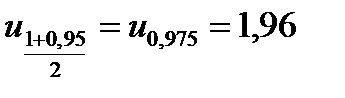 
):
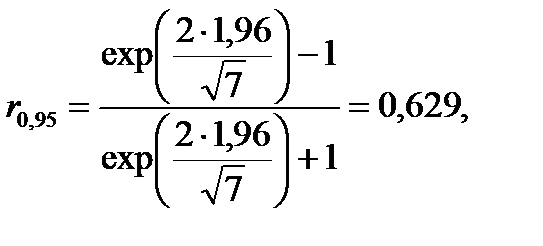
что близко к точному значению r0,95=0,632.
С помощью t-приближения получим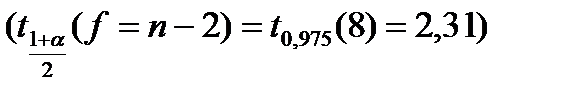 
:
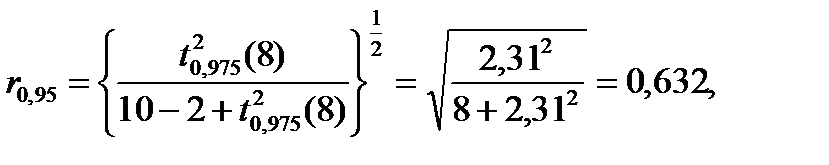
что совпадает с табличным значением
Наконец, приближение для больших выборок дает
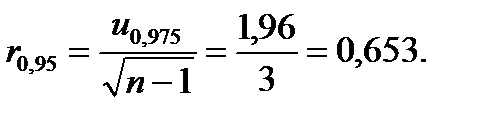
Дата добавления: 2018-11-25; просмотров: 391;