СТАТИСТИЧЕСКИЙ АНАЛИЗ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
Для оценки значимости коэффициента β регрессии y=α+βx можно воспользоваться следующими выражениями:
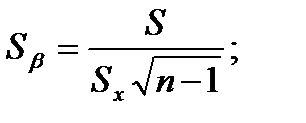 (4.72)
(4.72)
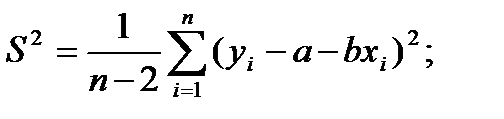 (4.73)
(4.73)
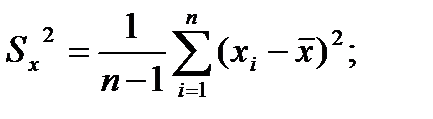 (4.74)
(4.74)
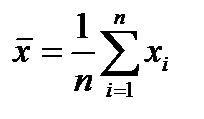 (4.75)
(4.75)
С помощью квантилей распределения Стьюдента можно проверить гипотезу о значимости коэффициента регрессии (существенности его отклонения от нуля), построить доверительный интервал для коэффициента β. Значение коэффициента β регрессия является значимым с достоверностью α, если:
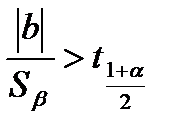 . (4.76)
. (4.76)
Двусторонний доверительный интервал для β имеет вид:
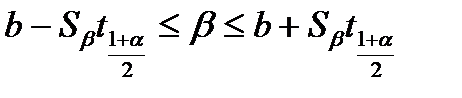 . (4.77)
. (4.77)
Проверка гипотезы о значимости коэффициента α и построение доверительного интервала для него выполняется по аналогии с коэффициентом β, при условии:
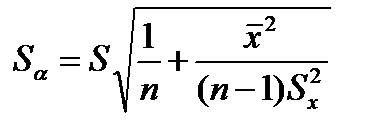 (4.78)
(4.78)
Пример: для совокупности данных найти оценки коэффициента α и β регрессии y=α+βx и провести их статистический анализ при доверительной вероятности α=0,95:
| xi | 1,2 | 2,4 | 2,8 | 4,2 | 5,9 | 6,8 | 8,1 | 9,2 | 10,1 | 11,0 |
| yi |
Вычисляем оценку β:
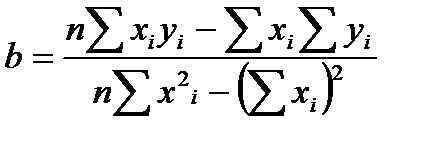 .
.
Имеем:
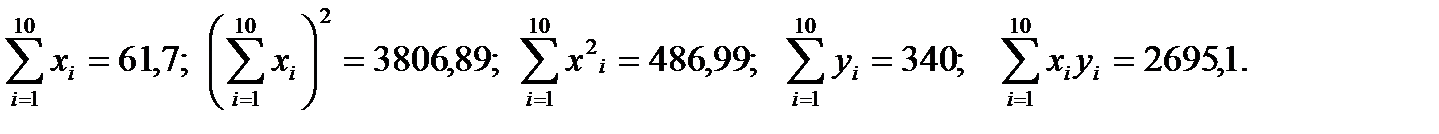
Тогда:
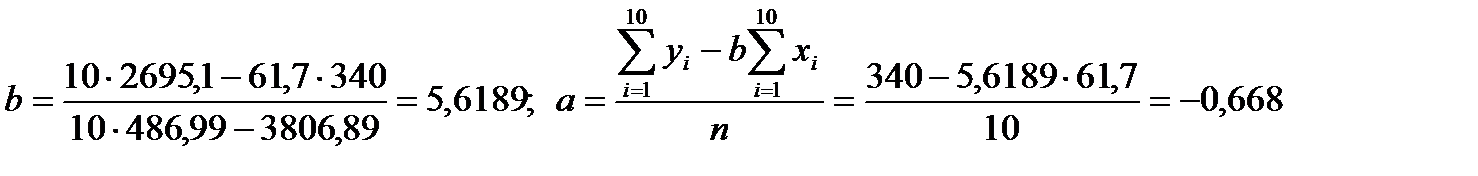
Проверим теперь значимость полученных коэффициентов (существенность их отклонения от нуля). Вычислим предварительно:
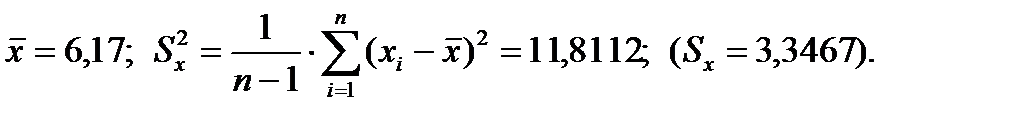
Далее вычисляем значение дисперсии:
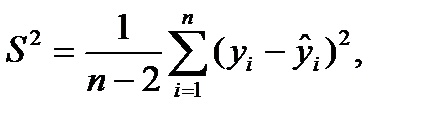
где 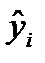 - расчетные значения, полученные при помощи уравнения регрессии.
- расчетные значения, полученные при помощи уравнения регрессии.
В нашем случае:
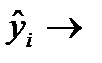 6,075; 12,818; 15,065; 22,932; 32,484; 37,541; 44,846; 51,027; 56,084; 61,141.
6,075; 12,818; 15,065; 22,932; 32,484; 37,541; 44,846; 51,027; 56,084; 61,141.
Вычисляем далее:
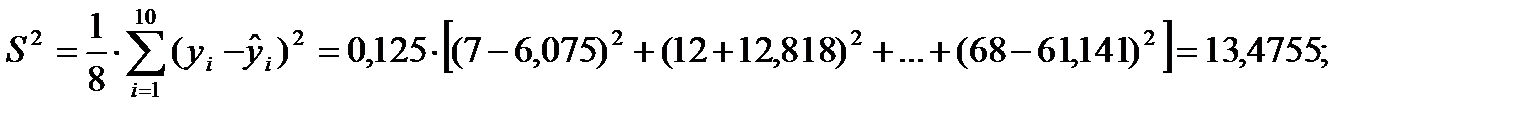
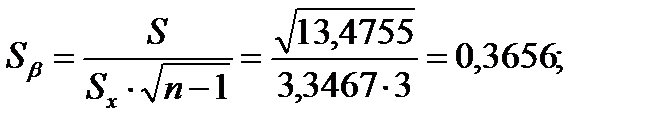
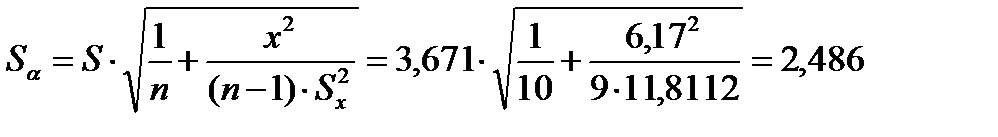
Для уровня достоверности α=0,95 имеем 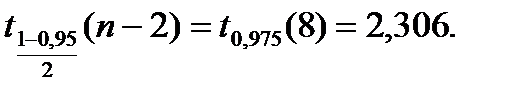
Проверяем значимость коэффициента β:
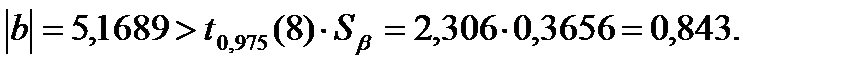
Следовательно, с достоверностью 0,95 делаем вывод о значимости коэффициента регрессии.
Доверительный интервал для β равен:
4,776≤β≤6,462
Аналогичные задачи решаем для коэффициента α:
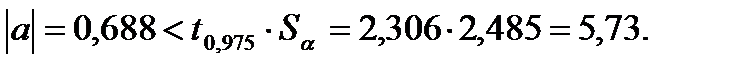
Следовательно, коэффициент α с вероятностью 0,95 не отличается от нуля, т.е. его значение может быть приравнено к нулю.
Таким образом, уравнение регрессии у по х адекватно отображается уравнением:
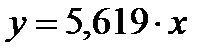 .
.
Дата добавления: 2018-11-25; просмотров: 538;
