ДВУХФАКТОРНАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ

Ранее рассматривались методы оценки и анализа линейной регрессии y=f(x). Если случайная величина у может зависеть одновременно от двух и более переменных, возникает задача оценки и анализа множественной регрессии:

y=f(x₁,x₂,…,x_k), (4.93)

где x_j (j-1,2,…,k) –независимые переменные.

Рассмотрим в качестве примера [12] регрессию y=α+β₁x₁+ β₂x₂ для случая двух независимых переменных x₁ и x₂. Для большего числа переменных оценки могут быть получены по аналогии. Для данного случая коэффициенты в уравнении регрессии определяются следующим образом:

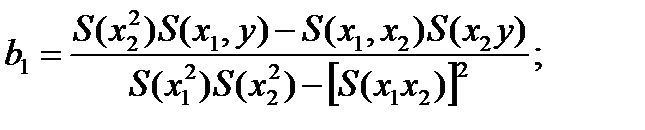(4.94)

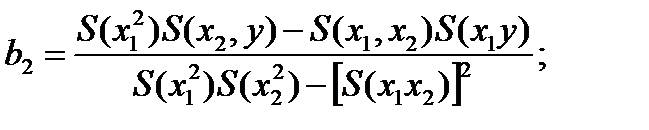(4.95)

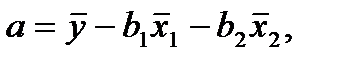(4.96)

где 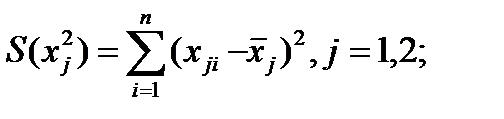(4.97)

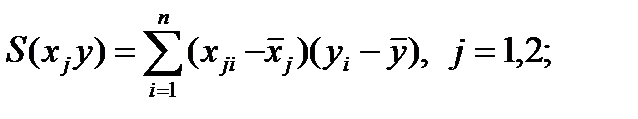(4.98)

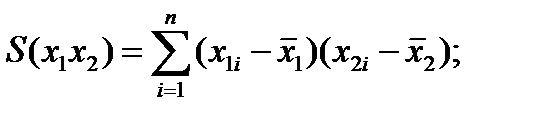(4.99)

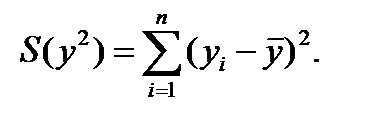(4.100)

Дисперсия, характеризующая разброс значений y_i вокруг линии регрессии, равна:

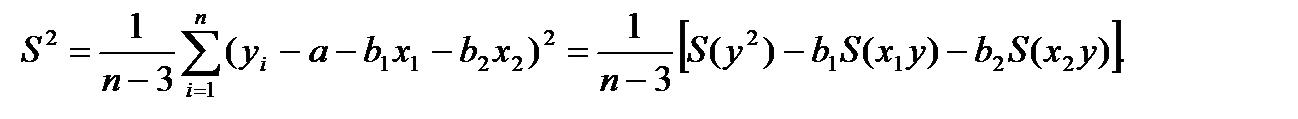(4.101)

Проверка значимости коэффициентов в уравнении регрессии (4.93) осуществляется по следующему алгоритму:

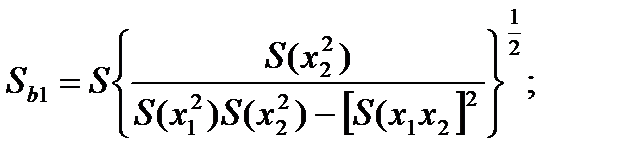(4.102)

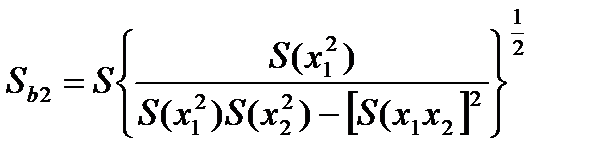(4.103)

Статистика t имеет распределение Стьюдента с f=n-3 степенями свободы.

Если:

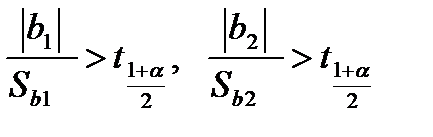, (4.104)

то коэффициенты b₁и b₂ признаются значимыми.

Сама регрессия признается значимой, если:

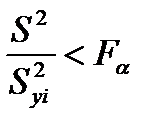, (4.105)

где 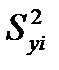- дисперсия значений y_i, оцениваемая по дублируемым наблюдениям.

Для F_α используются степени свободы f₁=n-3 и f₂=m-1, где m – объем выборки, по которой производилась оценка 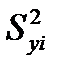. Табличные значения F_α определяются из соответствующей литературы, например [8].

Для большего числа независимых переменных расчеты и анализ множественной регрессии существенно усложняются. Однако, в настоящее время разработаны специальные методы планирования регрессионных экспериментов, позволяющие упростить расчет коэффициентов регрессии и сократить число необходимых экспериментов.