ОЦЕНКА КОРРЕЛЯЦИОННОГО ОТНОШЕНИЯ

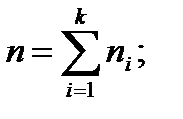
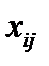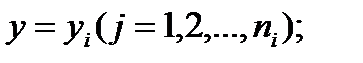
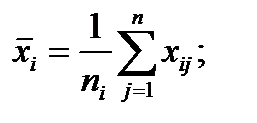
Предположим, что мы имеем n значений случайной величины y: y₁, y₂,…, y_k. При y=y_i наблюдаются n_i значений случайной величины х. Если - j-е значение величины х, наблюдаемое при 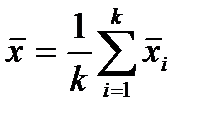, то выборочная оценка корреляционного отношения по х и у равна [12]:

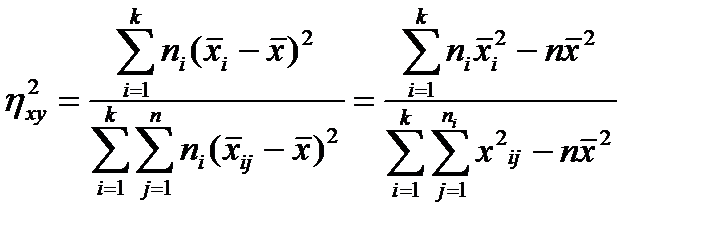(4.46)

Проверка гипотезы H₀: Ƞ²=0 против альтернативы H₁: Ƞ²≠0 производится с помощью статистики:

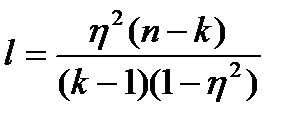. (4.47)

Если 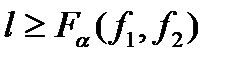, нулевая гипотеза отклоняется с достоверностью α. Здесь 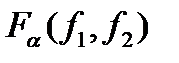- α-квантиль F-распределения с f₁=k-1 и f₂=n-k степенями свободы. При линейной связи между случайными величинами 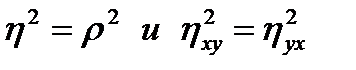. Следовательно, разность 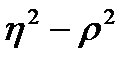может служить мерой нелинейной корреляционной связи. Проверка гипотезы H₀: 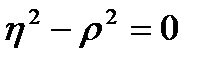против альтернативы H₁: 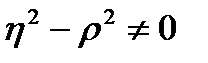может быть осуществлена с помощью статистики:

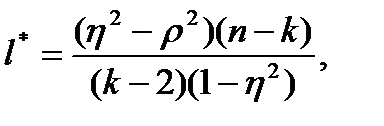(4.48)

имеющей при справедливости нулевой гипотезы F- распределение с f₁=k-2 и f₂=n-k степенями свободы. Если 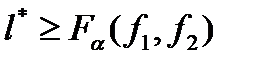, то с вероятностью α гипотеза линейной корреляционной связи отклоняется. Следует помнить, что для оценки корреляционной связи х по у необходимо иметь несколько наблюдений х для различных у (и наоборот).

Пример [12]: Проверить линейность корреляционной связи для выборки при доверительной вероятности α=0,95:

Имеем k=5, n_i=3 и n=15. Вычисляем далее:

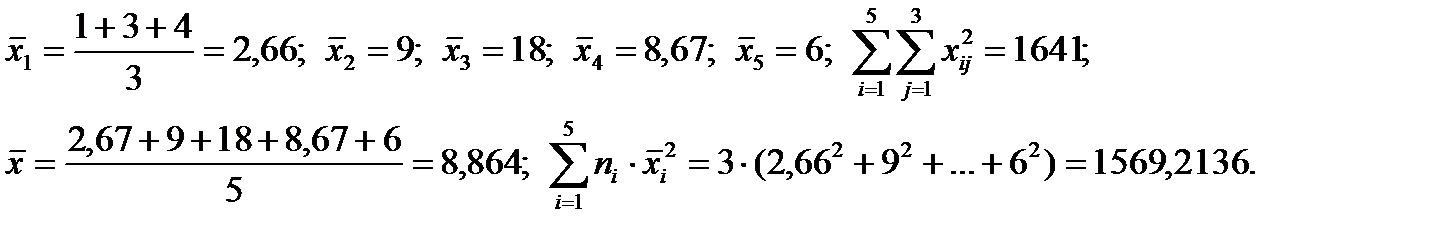
Тогда:

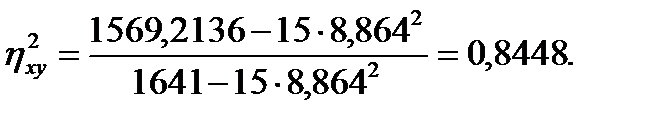
Из таблиц (например, [8]) находим F_0,95(f₁,f₂)= F_0,95(5-1;15-5)= F_0,95(4;10)=3,5.

Вычисляем далее: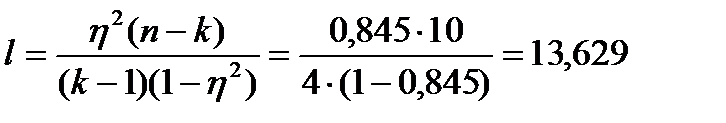

Полученная величина больше критического значения F_0,95(4,10)=3,5, следовательно, необходимо признать наличие существенной нелинейной связи междй х и у.

Оценим теперь отклонение связи между х и у от линейной, для этого оценим коэффициент корреляции. Вместо значений x_ij на каждом уровне y_j будем использовать средние значения x_i. Тогда ряд будет следующим:

х_i: 2,66 9 18 8,66 6

у_i: 2 4 9 13 15

Используя формулы из предыдущего раздела, получаем:

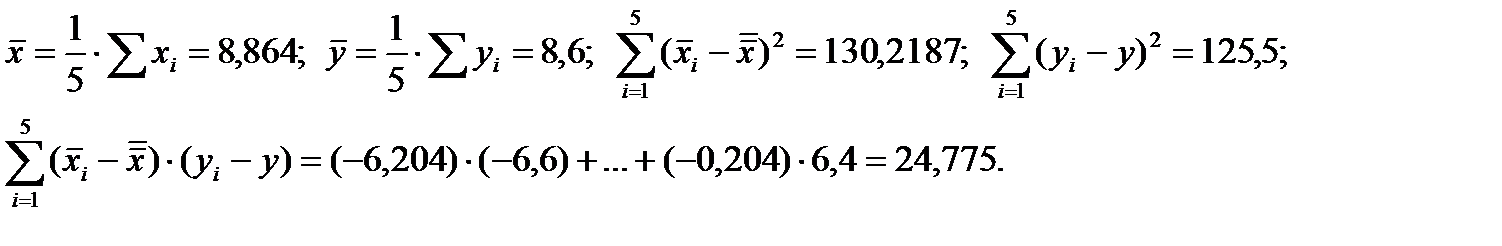
Тогда:

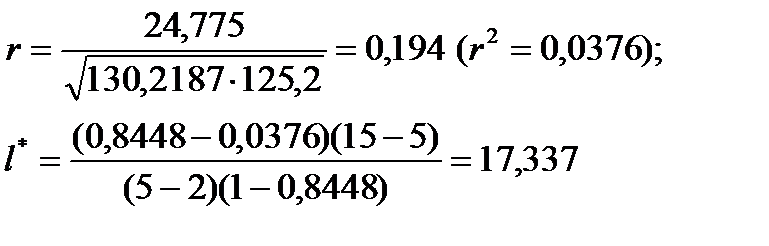
Из таблиц имеем F_0,95(5-2;15-5)=F_0,95(3;10)=3,7.

Так как l^*=17,337>F_0,95(3;10)=3,7, следует отклонить гипотезу о наличии линейной корреляционной связи между случайными величинами.

Вывод – незначимость коэффициента корреляции не означает отсутствия связи между исследуемыми величинами. Следует говорить об отсутствия линейной зависимости, так как незначимость коэффициента корреляции не исключает наличия нелинейной связи между случайными величинами.