ЧАСТНАЯ И МНОЖЕСТВЕННАЯ КОРРЕЛЯЦИЯ
При необходимости исследования связи между 3 и более случайными величинами используются частные и множественные коэффициенты корреляции. Рассмотрим случай трех переменных x,y и z (при числе переменных больше трех выражения для коэффициентов корреляции могут быть выписаны по аналогии).
Зависимость между двумя переменными х и у при фиксированной третьей переменной – z оценивается с помощью частного коэффициента корреляции pxy,z. По аналогии можно определить частные коэффициениы корреляции по остальным парам переменных pxz,ypzy,x.
Выборочные частные (парные) коэффициенты корреляции определяются с помощью соотношений [12]:
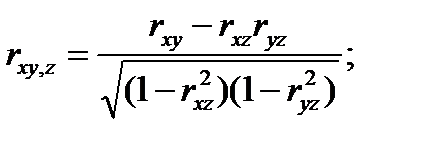 (4.49)
(4.49)
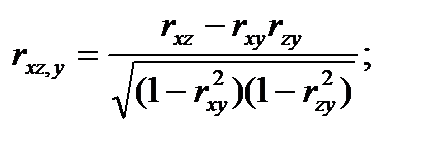 (4.50)
(4.50)
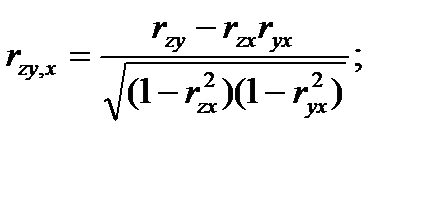 (4.51)
(4.51)
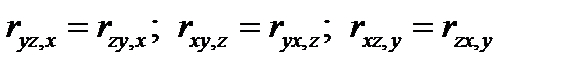 (4.52)
(4.52)
Так же, как и простые коэффициенты корреляции, парные коэффициенты принимают значения от -1 до +1 . Гипотеза Н0: pxy,z=0 для коэффициента корреляции pxy,z (для остыльных аналогично) проверяется с помощью статистики:
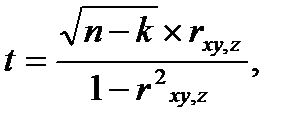 (4.53)
(4.53)
где k-число переменных (в нашем случае k=3).
При справедливости Н0 величина t распределена в соответствии с распределением Стьюдента при f=n-k степенях свободы.
Если :
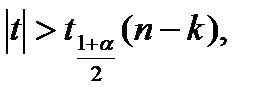 (4.54)
(4.54)
то нулевая гипотеза Н0 отклоняется с вероятностью α. Множественная корреляция исследуется в случае, когда необходимо установить существенность взаимосвязи одной переменной с совокупностью остальных. Выборочные множественные коэффициенты корреляциии обозначаются rx,yz, ry,xz, rz,xy и выражаются через парные коэффициенты корреляции с помощью соотношений:
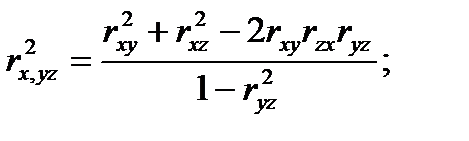 (4.55)
(4.55)
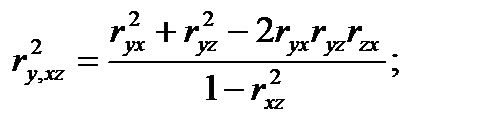 (4.56)
(4.56)
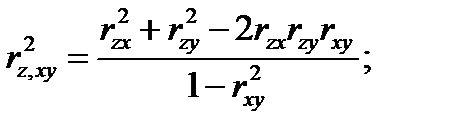 (4.57)
(4.57)
Между частными, множественными и обыкновенными парными коэффициентами корреляции имеют место, так называемые, контрольные соотношения:
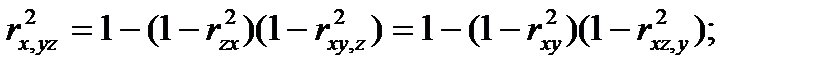 (4.58)
(4.58)
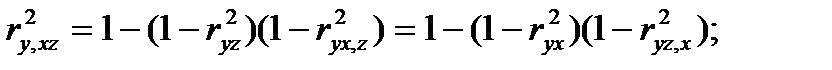 (4.59)
(4.59)
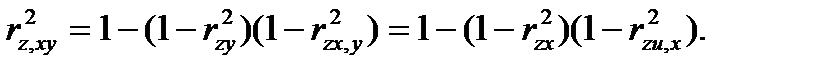 (4.60)
(4.60)
Для проверки гипотезы Н0: px,yz=0 используется статистика:
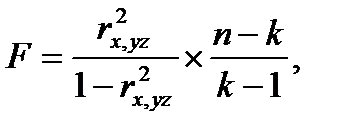 (4.61)
(4.61)
имеющая при справедливости Н0 F-распределение с f1=k-1 и f2=n-k степенями свободы (k-число переменных, в нашем случае k=3).
Таблица 4.14
Критические значения r1,23…k коэффициента множественной корреляции (k-число переменных, n-объем выборки)[12]
| n-k | Доверительная вероятность α | |||||||
| 0,95 | 0,99 | |||||||
| k | k | |||||||
| 0,999 0,975 0,930 0,881 0,836 0,795 0,758 0,726 0,697 0,671 0,648 0,627 0,608 0,590 0,574 0,559 0,545 | 0,999 0,983 0,950 0,912 0,874 0,839 0,807 0,777 0,750 0,726 0,703 0,683 0,664 0,646 0,630 0,615 0,601 | 0,999 0,987 0,961 0,930 0,898 0,867 0,838 0,811 0,786 0,763 0,741 0,722 0,703 0,686 0,670 0,655 0,641 | 1,000 0,990 0,968 0,942 0,914 0,886 0,860 0,835 0,812 0,790 0,770 0,751 0,733 0,717 0,701 0,687 0,673 | 1,000 0,995 0,977 0,949 0,917 0,886 0,885 0,827 0,800 0,776 0,753 0,732 0,712 0,694 0,677 0,662 0,647 | 1,000 0,997 0,983 0,962 0,937 0,911 0,885 0,860 0,837 0,814 0,793 0,773 0,755 0,737 0,721 0,706 0,691 | 1,000 0,997 0,987 0,970 0,949 0,927 0,904 0,882 0,861 0,840 0,821 0,802 0,785 0,768 0,752 0,738 0,724 | 1,000 0,998 0,990 0,975 0,957 0,938 0,918 0,898 0,878 0,859 0,841 0,824 0,807 0,791 0,776 0,762 0,749 |
Окончание таблицы 4.14
| n-k | Доверительная вероятность α | |||||||
| 0,95 | 0,99 | |||||||
| k | k | |||||||
| 0,532 0,520 0,509 0,488 0,470 0,454 0,439 0,425 0,373 0,308 | 0,587 0,575 0,563 0,542 0,523 0,506 0,490 0,476 0,419 0,348 | 0,628 0,615 0,604 0,582 0,562 0,545 0,529 0,514 0,455 0,380 | 0,660 0,647 0,636 0,614 0,594 0,576 0,560 0,545 0,484 0,406 | 0,633 0,620 0,607 0,585 0,565 0,546 0,529 0,514 0,454 0,377 | 0,678 0,665 0,652 0,630 0,609 0,590 0,573 0,557 0,494 0,414 | 0,710 0,697 0,685 0,663 0,643 0,624 0,607 0,591 0,526 0,442 | 0,736 0,723 0,712 0,690 0,669 0,651 0,633 0,618 0,552 0,467 |
Если F >Fα(f1,f2), то соответствующая корреляция признается значимой. Критическое значение коэффициента корреляции равно:
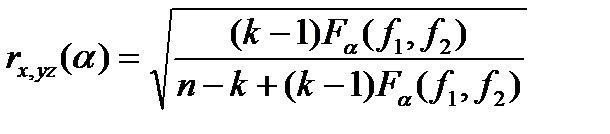 (4.62)
(4.62)
Корреляция признается значимой при rx,yz ≥ rx,yz(α). Критические значения r1,23…k (для общего случая k переменных) приведены в таблице 4.14.
Пример [12]: Вычислить коэффициенты частной и множественной корреляции и проверить из значимость при доверительной вероятности α=0,95 для данных, приведенных ниже (n=10, k=3)
| xi | ||||||||||
| yi | ||||||||||
| zi |
Найдем парные коэффициенты корреляции. Вычисляем коэффициент rxy:
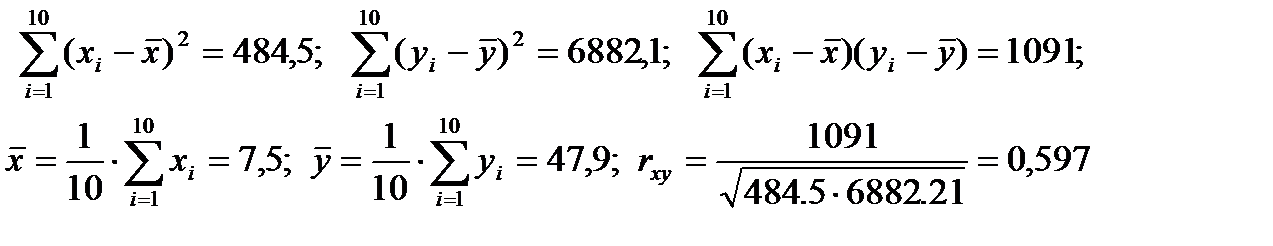
Вычисляем коэффициент rxz:
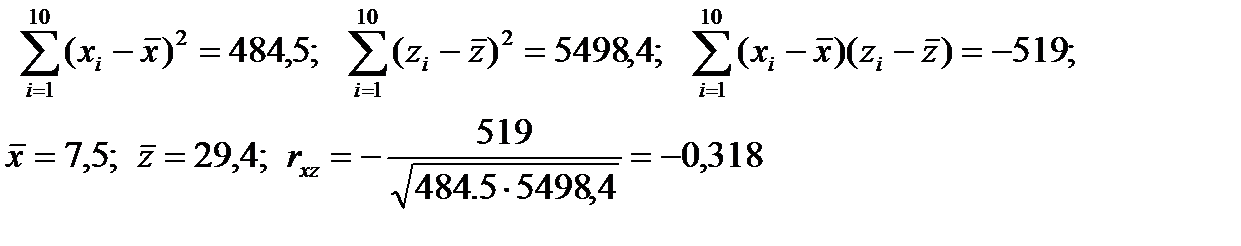
Вычисляем коэффициент ryz:
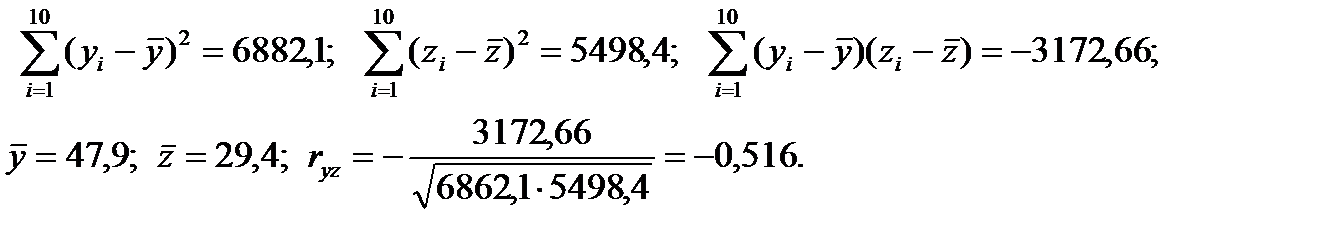
Вычислим теперь частные коэффициенты корреляции:

Вычислим множественные коэффициенты корреляции:
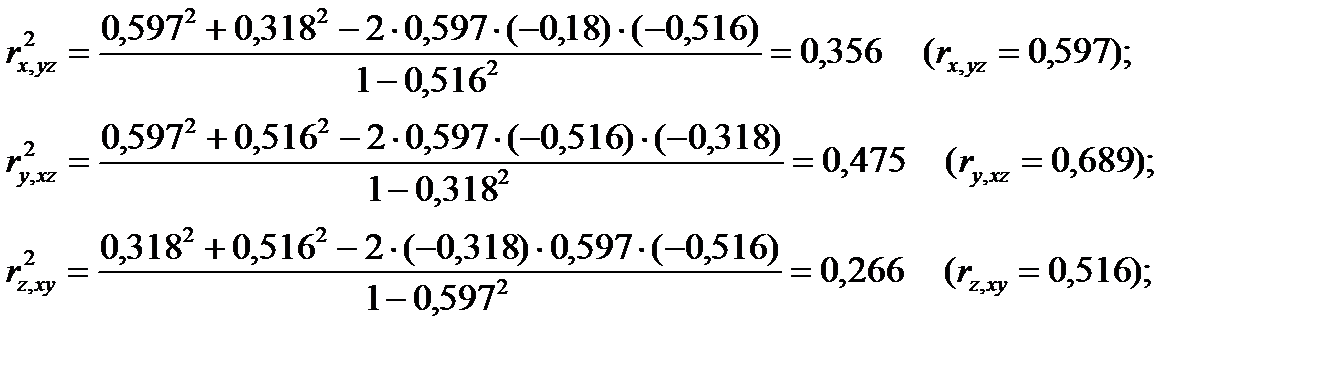
Вычислим t-статистики для проверки значимости частных коэффициентов корреляции:
- для проверки 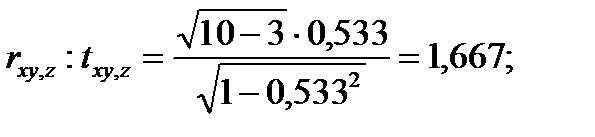
-для проверки 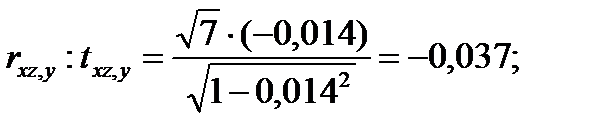
- для проверки 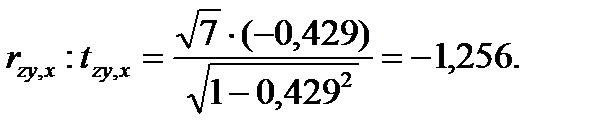
Для α=0,95 и f=n-k=7 из [4] для t-распределения имеем 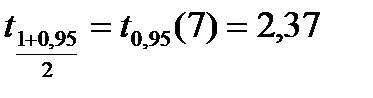 . Видим, что
. Видим, что 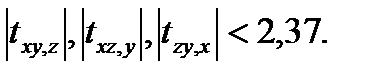
Следовательно, наличие частной корреляции отклоняется с достоверностью α=0,95.
Для коэффициентов множественной корреляции находим критическое значение (таблица 4.14) при k=3, n-k=7 и α=0,95. Имеем r1,23(0,95)=0,758.
Так как ни один множественный коэффициент корреляции (rx,yz=0,596 ry,xz=0,689 и rz,xy=0,516) не превышает критическое значение 0,758, то и наличие множественной корреляции отклоняется с достоверностью 0,95.
В заключении проверим правильность вычислений, используя контрольные соотношения:
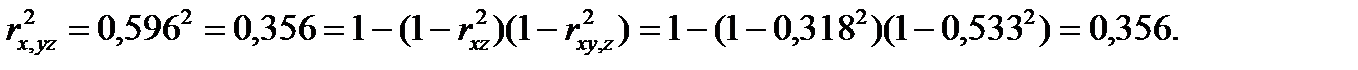
4.3. РЕГРЕССИОННЫЙ АНАЛИЗ [12, 13, 14]
Рассмотренные ранее методы дисперсионного и корреляционного анализа позволяют выявить наличие связи между случайными величинами и оценить силу этой связи.
Следующей ступенью является выявление конкретного функционального вида связи между случайными величинами.
При наличии корреляционной связи между у и х имеет место соотношение F(y)=F(x,y), т.е. функция распределения случайной величины у зависит от значения случайной величины х.
Наибольший практический интерес представляет определение зависимости 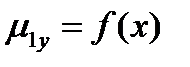 ,описывающей истинную зависимость между у и х. Зависимость средних значений
,описывающей истинную зависимость между у и х. Зависимость средних значений 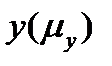 называется регрессией у по х, а методы нахождения таких зависимостей и оценки их статистических свойств составляют содержание регрессионного анализа.
называется регрессией у по х, а методы нахождения таких зависимостей и оценки их статистических свойств составляют содержание регрессионного анализа.
По выборочным данным можно найти только оценку истинной регрессии, содержащую ошибку, связанную со случайностью выборки.
В основе регрессионного анализа лежит принцип наименьших квадратов, в соответствии с которым в качестве уравнения регрессии y=f(x) выбирается функция, доставляющая минимум сумме квадратов разностей:
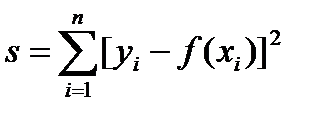 . (4.63)
. (4.63)
Как правило, вид функции f(x) определяется заранее, а методом наименьших квадратов определяются ее коэффициенты, минимизирующие S. Количественной мерой рассеяния значений yi вокруг регрессии f(x) является дисперсия:
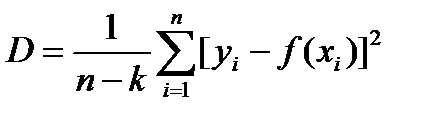 (4.64)
(4.64)
где k – число коэффициентов, входящих в аналитическое выражение регрессии (например, если f(x) – многочлен степени L, то k=(L+1).
В зависимости от вида уравнения регрессии у = f(x) различают линейную (f(x) – многочлен первой степени) и нелинейную (f(x) – многочлен степени ≥2) регрессии.
Вид функции f(x) выбирается исходя из особенностей исследуемого явления (процесса), а так же из общего графического анализа зависимости между у и х.
Чаще всего ограничиваются рассмотрением линейной регрессионной модели, а при нелинейной зависимости у=f(x) используют различные линеаризующие преобразования переменных у и х. Наиболее распространенные из этих преобразований приведены в табл. 4.15 [12].
Схема регрессионного анализа включает в себя последовательное решение следующих задач [12, 13, 14]: нахождение выборочной оценки истинной регрессии, оценка статистической значимости выборочной регрессии в сравнении с безусловным разбросом значений уi, характеризующимся дисперсией σу2; определение доверительных областей, с заданной вероятностью включающих в себя истинную регрессию.
Таблица 4.15
Линеаризующие функциональные преобразования (у*=а*+b*x*)
| Исходная зависимость у= f(x) | Преобразование переменных | Преобразование коэффициентов | ||
| у* | х* | а* | b* | |
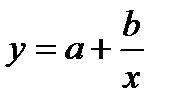
| y |  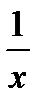
| a | b |
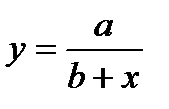
| 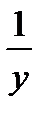
| x | 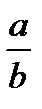
| 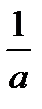
|
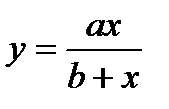
| 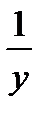
| 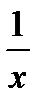
| 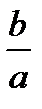
| 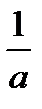
|
Окончание таблицы 4.15
| Исходная зависимость у= f(x) | Преобразование переменных | Преобразование коэффициентов | ||
| у* | х* | а* | b* | |
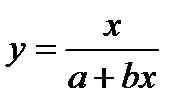
| 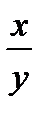
| x | a | b |
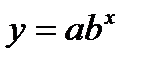
| lgy | x | lga | lgb |
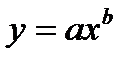
| lgy | lgx | lga | b |
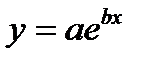
| lny | x | lna | b |
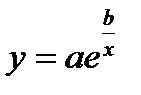
| lny | lna | b |
Среди дополнительных задач, позволяющих получить полную статистическую картину изучаемой регрессии, отметим [12]: анализ регрессионных остатков (разница между выборочной регрессией и выборочными значениями функции); анализ наличия грубых отклонений от регрессии (выбросов); построение толерантных границ для регрессии. Разработанный в настоящее время аппарат регрессионного анализа предполагает, что значения уi взаимно независимы и нормально распределены. Выполнение этих условий должно быть предварительно проверено с помощью критериев нормальности (см. раздел 4) и критериев сравнения дисперсий (см. раздел 4).
ЛИНЕЙНАЯ РЕГРЕССИЯ
Линейный регрессионный анализ исходит из наличия зависимости 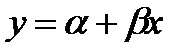 , где α и β – неизвестные коэффициенты регрессии. Выборочные оценки α и β в дальнейшем будем обозначать a и b соответственно.
, где α и β – неизвестные коэффициенты регрессии. Выборочные оценки α и β в дальнейшем будем обозначать a и b соответственно.
Определение коэффициентов регрессии методом наименьших квадратов:оценки наименьших квадратов являются решениями системы нормальных уравнений, строящихся по совокупности наблюдаемых значений уi для совокупности значений хi [12, 13, 14]:
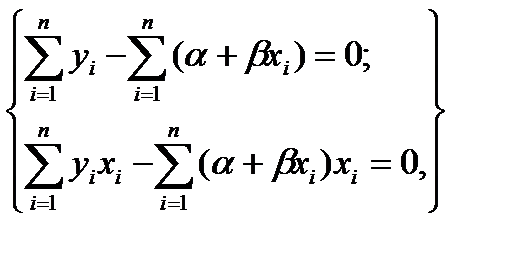 (4.65)
(4.65)
из которой следует система:
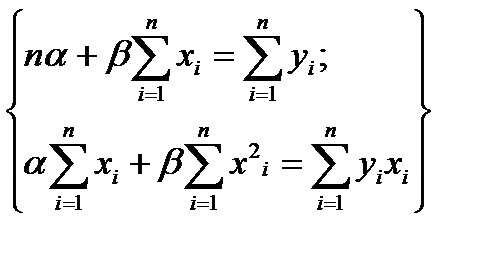 (4.66)
(4.66)
Решение системы дает искомые оценки коэффициентов регрессии:
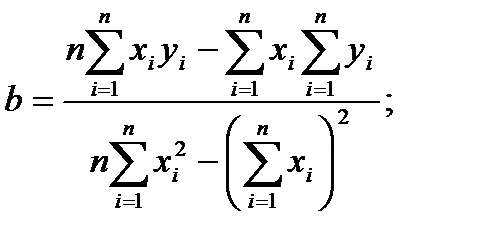 (4.67)
(4.67)
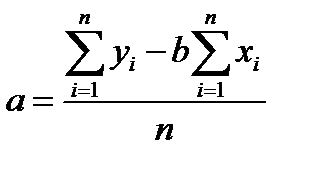 (4.68)
(4.68)
Для проверки правильности вычислений можно использовать соотношение:
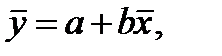 (4.69)
(4.69)
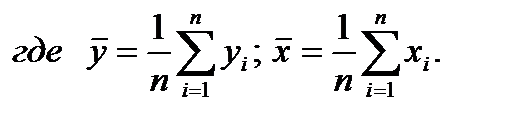
Вычисления a и b существенно упрощается, если интервалы между значениями независимой переменной х постоянны, т.е. если хi+1 - xi=const (i=1,2,…,n-1). В работе [12] представлен экономичный линейный метод оценивания, который при незначительной потере в точности позволяет существенно сократить время вычислений. Эти оценки имеют вид:
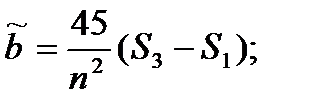 , (4.70)
, (4.70)
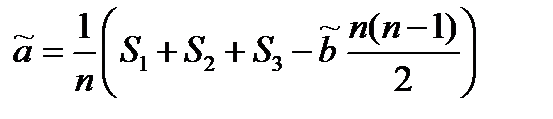 (4.71)
(4.71)
где 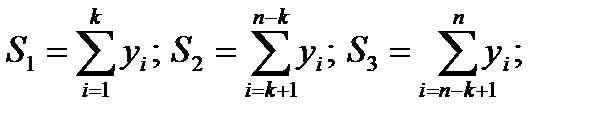 k – ближайшее целое к
k – ближайшее целое к 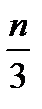 .
.
Пример [12]: в результате наблюдений за зависимостью y=f(x) получены следующие данные:
| yi | ||||||||||
| xi |
Необходимо найти оценки коэффициентов регрессии у по х методом наименьших квадратов.
Находим:
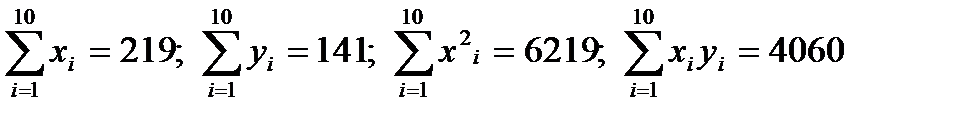 .
.
Далее вычисляем оценки:
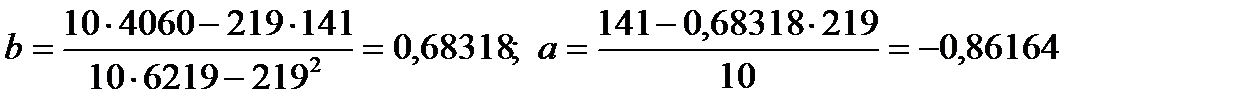 .
.
Следовательно, уравнение регрессии у по х имеет вид:
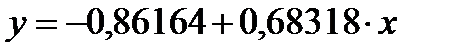 .
.
Пример [12]:в результате наблюдения за зависимостью y=f(x) получены следующие данные:
| yi | |||||||||||||||
| xi |
Необходимо найти оценки коэффициентов регрессии у по х.
Воспользуемся линейными оценками. Примем k=n/3=5 и вычисляем:
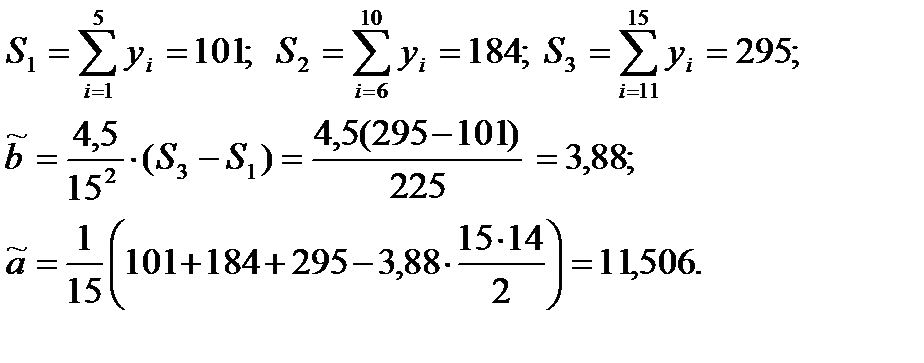
В случае нелинейной модели форму 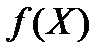 нам должны подсказать - теория, интуиция, опыт, анализ эмпирических данных и т.д. Выбор формы зависимости можно осуществить при помощи графического анализа материала наблюдений. Одним и тем же условиям могут удовлетворять несколько различных функций (ниже представлены примеры таких функций [10]).
нам должны подсказать - теория, интуиция, опыт, анализ эмпирических данных и т.д. Выбор формы зависимости можно осуществить при помощи графического анализа материала наблюдений. Одним и тем же условиям могут удовлетворять несколько различных функций (ниже представлены примеры таких функций [10]).
| 
|
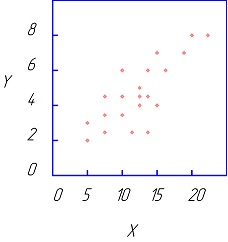
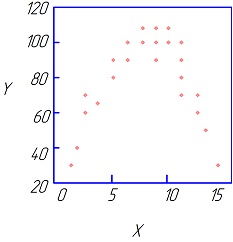
| Рис. 4.2 Линейная зависимость Y=α+βX+ε. | Рис. 4.3 Квадратичная зависимость: Y=α+βX+γX2+ε |
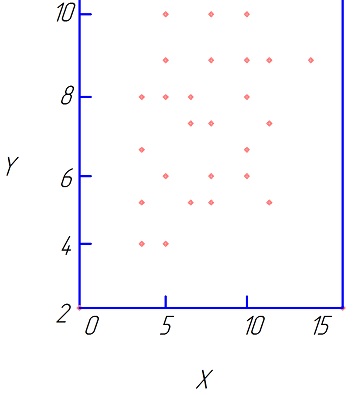
| 
|
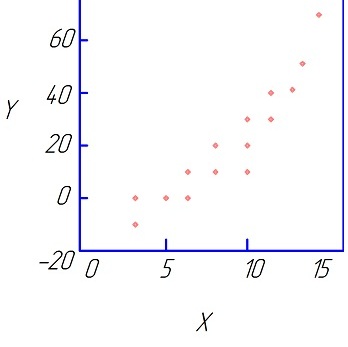
| Рис.4.4 Степенная зависимость Y=AeβXε | Рис. 4.5 X и Y независимы |
Нас интересуют только те формы зависимости, которые путем преобразования переменных и параметров можно свести к линейным. Т.е. после преобразования переменных и коэффициентов новые переменные и ошибка будут связаны линейным соотношением.
4.3.2. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ РЕГРЕССИОННОЙ МОДЕЛИ [10, 12, 13, 14, 15]
Дата добавления: 2018-11-25; просмотров: 1153;
