Корреляция между компонентами в рудах месторождений полезных ископаемых.
В математической статистики количественная связь между признаками, явлениями или компонентами оценивают методом корреляции. При статистической обработке данных полученных в результате геологоразведки для научных и практических выводов важно проследить, как меняются значения в пробах одного компонента относительно другого, то есть нужно найти уравнение связи и значение коэффициента корреляции, определяющего степень влияния одного компонента на другой компонент.
Термин “correlation” – переводится с английского языка как соотношение, сопоставление или взаимозависимость. Связи между компонентами, проявляющиеся в изменение одного компонента относительно другого компонента называют статистическими, в отличие от функциональных связей, где влияние одного признака на другой происходит по формуле. В статистических связях влияние изменения одного компонента на изменение другого проявляется в среднем, при этом отдельные результаты могут противоречить установленной связи.
В большинстве геологоразведочных данных наблюдается, что в пробах измеряется сразу несколько компонентов. Например, в некоторых пробах измерялись содержания хрома, никеля и ванадия. Результаты опробования представлены в таблице 3333.
Таблица
| CR | NI | V |
| Сумма - 1110 | Сумма - 675 | Сумма - 935 |
| Среднее - 222 | Среднее - 135 | Среднее - 187 |
Эти компоненты могут и не быть независимыми друг от друга, между ними может существовать некоторая статистическая связь. Как оценить силу этой связи и если сама эта связь между этими компонентами. Для оценки силы связи можно использовать вычислительные процедуры, которые мы используем для вычисления дисперсии, только не одного компонента, а для пары компонентов. Вычисление дисперсии сразу для пары компонентов называется ковариацией (в английском языке variation - дисперсия covariation – совместное изменение двух величин) и является характеристикой совместного изменения двух переменных по отношению к их общему знаменателю.
Это соотношение можно изобразить на рисунке двойной гистограммы в трехмерном пространстве.
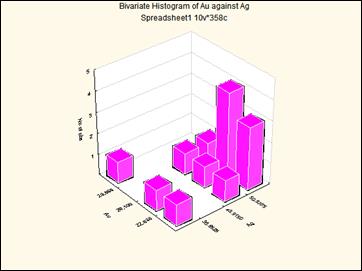
Рис. Вид двойной гистограммы в трехмерном пространстве.
Точно как дисперсия характеризует разброс относительно центральной точки, ковариация характеризует разброс значений относительно общего среднего распределений двух компонентов.
Вычисление оценки ковариации прямо вытекает из вычисления оценки дисперсии. Формула дисперсии –
- S2=1/n1∑(xiχ)2 – переписывается как S2=1/n1∑(xiχ)*(xiχ) и далее преобразуется для двух компонентов, например - Cov=1/n1∑(xCrχCr)*(xNiχNi). Если, например значения в пробах хрома и никеля будут равны то формула ковариации (COV) сведется к формуле дисперсии (S2), то есть формула ковариации является частью формулы дисперсии. Можно вычислить дисперсии и ковариации для компонентов, представленных в таблице и из вычисленных значений составить новую таблицу.
Таблица
| Cr | Ni | V | |
| Cr | S2(Cr) | Cov (Cr-Ni) | Cov (Cr-V) |
| Ni | Cov (Ni-Cr) | S2(Ni) | Cov (Ni-V) |
| V | Cov (V-Cr) | Cov (V-Ni) | S2(V) |
Формула ковариации позволяет очень чутко реагировать на скорость изменения одного компонента относительно скорости изменения другого. Это хорошо иллюстрирует следующий цифровой пример, в таблицах № 1 и 2 в котором расчеты приведены без усредняющего фактора по формуле - ∑(xCrχCr)*(xNiχNi).
Таблица 1
| Сr | Ni | (xCrχCr)*(xNiχNi) |
| (5-10)*(25-30)=25 | ||
| (10-10)*(30-30)=0 | ||
| (15-10)*(35-30)=25 | ||
| ∑(xCrχCr)*(xNiχNi) |
Таблица 2
| Сr | Ni | (xCrχCr)*(xNiχNi) |
| (5-10)*(25-28)=15 | ||
| (10-10)*(28-28)=0 | ||
| (15-10)*(30-28)=10 | ||
| ∑(xCrχCr)*(xNiχNi) |
Анализ этих двух таблиц показывает, что если увеличение одного компонента сопровождается меньшим увеличением другого компонента, то сумма становится значительно меньше.
На рисунке, расположенном ниже приведен график совместного распределения двух компонентов, тесно связанных между собой, и которые имеют высокие значения ковариации.
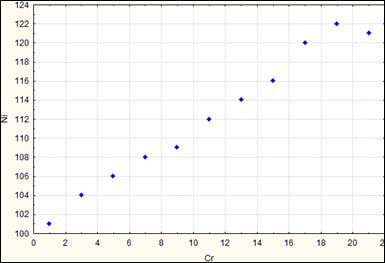
Рис. Совместное распределение двух компонентов, тесно связанных между собой.
На следующем рисунке приведен график совместного распределения двух компонентов, которые имеют те же дисперсии, но абсолютно не зависят друг от друга.
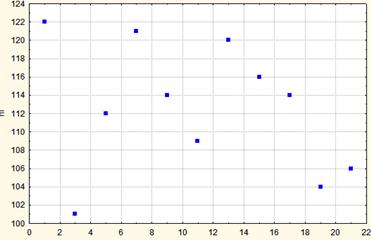
Рис. Совместное распределение двух компонентов, абсолютно не связанных между собой, но имеющих те же дисперсии.
Однако анализ дисперсий и ковариаций не так удобен, так как значения этих статистик зависит от единиц измерения и трудно проводить сравнения распределений значений проб компонентов, если например одни компоненты измеряются в процентах, а другие в граммах на тонну. Для оценки степени взаимной связи между компонентами (переменными) используется коэффициент корреляции, который представляет собой отношение ковариации двух компонентов к произведению их стандартных отклонений.
R= Cov(Ni-Cr)/Sni*SCr
Если значения проб никеля и хрома равны между собой, то в числителе и знаменателе мы получим значения дисперсии, и отношение станет равным единице. Поэтому крайнее значение коэффициента корреляции приближается к единице, но не достигает ее, так как если связь между компонентами будет равна единице, то это будет указывать на наличие прямой линейной связи между двумя переменными, и такая связь не будет статистической, и не будет называться корреляционной. Коэффициент корреляции – называют линейным коэффициентом корреляции, и он принимает значения от -1 до +1. Если коэффициент корреляции приближается к -1, то это указывает на отрицательную связь, то есть в этом случае одна переменная изменяется в противоположном направлении по отношению к другой. Между двумя упомянутыми случаями находится спектр менее сильных связей, если коэффициент корреляции находится около нуля или равен нулю, то это указывает на полное отсутствие статистических линейных зависимостей. На рисунках 44 44 44 изображены различные ситуации.
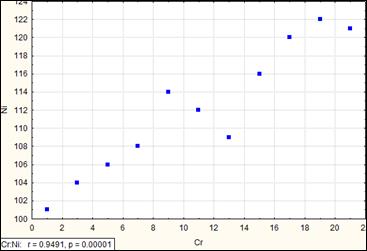
Рис. Коэффициент корреляции равен 0.95 (сильная корреляция)
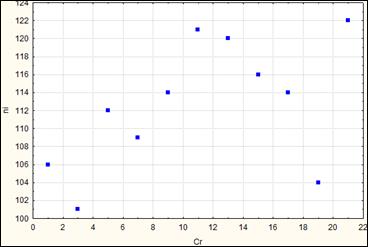
Рис. Коэффициент корреляции равен 0.54 (менее очевидная корреляция или слабая корреляция)
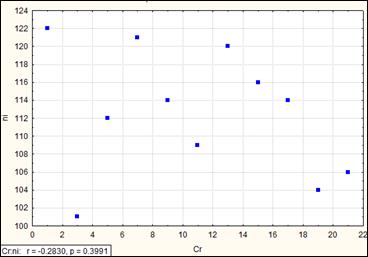
Рис. Коэффициент корреляции равен -0.28 (почти полное отсутствие корреляции).
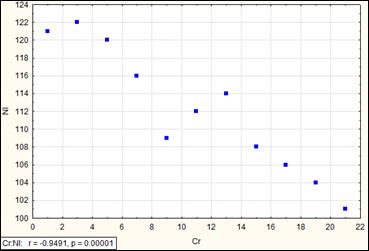
Рис. Коэффициент корреляции равен -0.95 (отрицательная корреляция, одна переменная уменьшается, другая увеличивается).
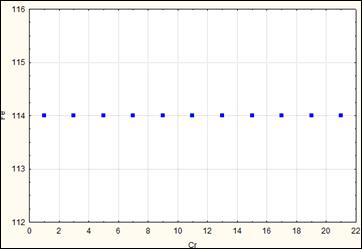
Рис. Коэффициент корреляции подсчитать нельзя, так как у одной из переменных не меняются значения и стандартное отклонение равно 0, при вычислении коэффициента корреляции происходит попытка деления на 0.
Коэффициент корреляции нельзя определить, если на графике мы видим не линейное распределение компонентов относительно друг от друга, а близкое к кругу, экспоненте, или квадратичной кривой, в этом случае можно предположить связь между переменными (компонентами), но эта связь не является линейной, а коэффициент корреляции фиксирует только степень линейной связи. Существует много возможных не линейных зависимостей между переменными, но в этом случае коэффициент корреляции нельзя считать удовлетворительной мерой степени связи между переменными. Так как коэффициент корреляции измеряет линейное соотношение между двумя переменными, то можно рассчитать формулу прямой, характеризующей зависимость между ними.
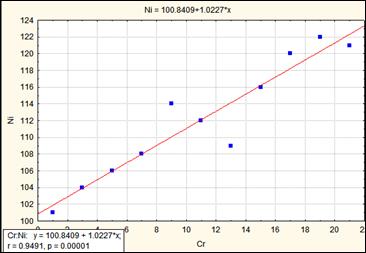
Рис. Прямая – характеризует связь между компонентами.
Используя эту формулу можно рассчитать примерное значение второго компонента относительно положения первого в новых пробах. Установление четкой линейной связи может позволить в некоторых случаях сэкономить на опробовании попутных компонентов.
Дата добавления: 2019-04-03; просмотров: 648;
