Основные методы интерполяции.

Данные, с которыми приходится иметь дело геологам, непосредственно связаны с пространством, то есть каждая проба имеет пространственные координаты. Положение данных фиксируется в пространстве на планах и разрезах. Уже здесь геологи получают первичную информацию о равномерности опробования, наличии богатых и бедных зон. Более полную информацию несет в себе карта изолиний переменной по значениям в пробах. Анализируя карту изолиний, например полезного компонента можно более определенно выделять зоны с повышенной и пониженной изменчивостью компонента, зоны с более высоким или более низким его содержанием. Однако перед построением самой простой карты изолиний желательно привести пункты наблюдений к равномерному виду, так как иначе мы будем получать значительную ошибку при интерполяции в местах, где точек наблюдения меньше. Эту задачу в нашей стране решал Делонэ. Он усовершенствовал метод классической триангуляции, предложив способ построения треугольников для последующего интерполирования, в котором стороны равны настолько насколько это возможно. Он вслед за Тиссеном ввел понятие естественного соседа для двух наиболее близко расположенных точек наблюдения. Если провести через эти две точки окружность, то первая точка, которая попадет в этот круг и будет естественным соседом, стороны вновь образованного треугольника в этом случае будут почти равны или будут наиболее равными из всех других возможных вариантов. Однако были выдвинуты другие идеи приведения точек наблюдения к равномерному виду. Наибольшее значение получила идея приведения неравномерно расположенных точек наблюдения в равномерно расположенные точки по сети или гриду (grid) через сглаживание, а сама эта процедура получила название gridding. Одним из первых, кто предложил эту методологию, был южноафриканский геолог Дени Криге. Он обратил внимание, что содержание золота в блоке после отработки было с более низким содержанием, чем по разведочным данным и предложил проводить сглаживание скользящим окном и рассчитывать для блока скользящее среднее, что являлось лучшей оценкой истинного среднего в отрабатываемом блоке. Рекомендуется проводить трехкратное сглаживание. Сглаживание, при котором убираются пики значений признаков, еще называют фильтрацией. В технике известны фильтры более 100 разновидностей. Один из самых простых фильтров – это трехчленный фильтр Шеппарда, ранее Каллистов рекомендовал использовать пятичленный фильтр Шеппарда, в котором используются не равные коэффициенты перед значениями. Позднее Матерон – основатель геостатистики предложил геологическое сглаживание называть кригингом в честь Дени Криге.

Расчет значения средних точек грида или блоков для трехмерного случая и есть задача интерполирования. Среди многочисленных методов интерполирования наибольшее развитие получили несколько методов.

1. Полигональный метод. Если есть рассеянное множество точек, то можно представить, что каждая точка, лежащая внутри многоугольника, расположена ближе к любой другой точке, содержащейся в ней, чем в точке вне его. В этом случае содержание компонента внутри элементарного многоугольника присваивается от пробы, находящейся в середине данного многоугольника. Множества многоугольников с такими свойствами называют многоугольниками Тиссена, Дирихле, Вороного. Модель Вороного является трехмерным обобщением многоугольников (примером является совокупность мыльных пузырей). К полигональному методу близок метод - триангуляция Делоне.

2. Метод ближайшего соседа (Nearest Neighbour – этот метод реализован в программе Datamine Studio). В трехмерных программах типа Datamine Studio значения интерполируются в центры элементарных блоков (cells) в блочных моделях, а не в центр многоугольника. Значение в середине блока присваивается от ближайшей пробы, находящейся вблизи данного элементарного блока. По сути метод ближайшего соседа является заменой полигонального метода, в котором содержания компонента интерполируются не в многоугольные блоки разного размера (разный размер блоков возникает из-за неравномерности разведочной сети), а в равные по размерам элементарные блоки (sells) блоковой модели, ограниченной каркасом рудного тела.

3. Метод обратных расстояний (Inverse Power of Distance - этот метод реализован в программе Datamine Studio). Оценивание содержания в блоке методом обратных расстояний основано на формуле:

𝑥 = (𝑥1/d1²+𝑥2/d2²+𝑥3/d3²…..) / ( 1/d1² + 2/d2² + 3/d3²…..),

где 𝑥 – это содержание компонента, а d² – это расстояние от пробы до середины интерполируемого блока в квадрате.

Предполагается, что при интерполяции, при расчете значения в конкретном блоке будут участвовать все пробы, попадающие в эллипсоид поиска, но большее влияние при расчете будут иметь близко расположенные пробы, и наименьшее влияние будут оказывать пробы расположенные на удалении. Этот метод интерполяции сейчас самый популярный в мире и наиболее часто используется. Большое значение в этом методе имеет степень (Power), которая принимается для вычислений в каждом конкретном случае (в большинстве случаев принимается вторая степень). (Смотри рис. № ).

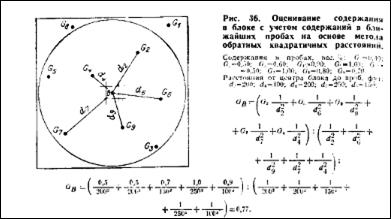
Рис.№ . Рисунок показывает механизм расчета оценки содержания компонента в элементарном блоке методом обратных расстояний (из книги Мишеля Давида).

4. Кригинг и его разновидности (ordinary kriging- обыкновенный кригинг, simple kriging – простой кригинг – этот метод реализован в программе Datamine). При его применении необходим анализ вариограмм, так как характеристики вариограммы и используются в уравнении, рассчитывающем интерполяционные оценки блоков.

5. Метод оценки Сишела (Sichel’s T Estimator). Этот метод используется для интерполяции непараметрических массивов данных.