Критерий Колмогорова-Смирнова.
Критерий Колмогорова-Смирнова используется для проверки выборочного распределения, является ли оно нормальным распределением и может служить альтернативой χ2 критерию. Этот критерий так же используется для проверки гипотезы о нормальном распределении данных, измеренных в разных шкалах измерения. Самое большое преимущество критерия Колмогорова-Смирнова, что данные не нужно группировать в произвольные группы, как в случае с χ2 критерием. Выборочная и нормальная модель распределения наносится на один график в кумулятивной форме или сравнивается в одной частотной таблице как в данном примере.
| Содержание Cu % | Частоты выборочного распределения | Частоты нормального распределения | Накопленные частоты выборочного распределения | Накопленные частоты нормального распределения | Разница частот |
| 56-58 | |||||
| 58-60 | |||||
| 60-62 | |||||
| 62-64 | |||||
| 64-66 | |||||
| 66-68 | |||||
| 68-70 | |||||
| 70-72 | |||||
| 72-74 |
Обычно критерий Колмогорова-Смирнова используется в тех случаях, когда сравниваются распределения с известными истинными параметрами. Расчет этого критерия был усовершенствован Лиллиефорсом, что позволило применять метод, используя оценки среднего и дисперсии в выборочном распределении и рассчитывать критерий примерно по той же схеме, как мы рассчитывали критерий Пирсона (χ2 критерий). Предварительно все выборочные данные, полученные в результате нашего эксперимента (или опробования), стандартизируются, и записываются в частотную таблицу в обычном и накопленном виде. Для тех же границ интервалов, что и в нашем экспериментальном распределении, в таблице нормального распределения находятся частоты и так же записываются в обычном и накопленном виде. Затем находится наибольшая разница D и критерий Колмогорова-Смирнова рассчитывается по следующей формуле –
λ = D/√n.
где D – максимальное значение разности между накопленными эмпирическими и теоретическими частотами, n – количество данных в выборке или общее количество всех частот в выборочном (эмпирическом) распределении.
Величина критерия в данном случае будет равна λ = 0.31. Обычно полученную таким образом величину сравнивают с опубликованными рассчитанными величинами критерия для разных степеней свободы и уровня риска. Из пояснений к таблице Колмогорова, если число проб (n) превышает 100, то для 95% вероятности асимптотическая граница находится по формуле 1.36/√n, в данном случае асимптотическая граница равна 0.06, что значительно меньше вычисленного значения и соответственно с вероятностью в 95% можно отвергнуть в данном случае нулевую гипотезу. Если же рассчитанная исследователем величина не превышает значение в таблице, то и нет оснований отвергать нулевую гипотезу. Однако у этого метода есть ограничение – наибольшую разницу между частотами нужно искать в середине кумулятивного графика или частотной таблицы, определение наибольшего расхождения в начале и конце графика может привести к ошибочному выводу и для лучшего результата число проб должно быть больше чем 100.
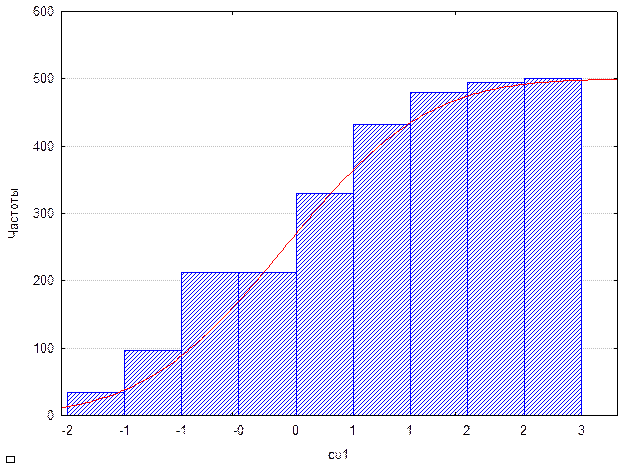 Рис. Сравнение выборочного распределения и нормального теоретического распределения для расчета критерия Колмогорова-Смирнова.
Рис. Сравнение выборочного распределения и нормального теоретического распределения для расчета критерия Колмогорова-Смирнова.
Дата добавления: 2019-04-03; просмотров: 1806;
