Критерий Байеса-Лапласа
Обозначим через 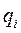 – вероятность появления внешнего состояния Fj.
– вероятность появления внешнего состояния Fj.
Соответствующее правило выбора можно интерпретировать следующим образом: матрица решений 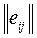 дополняется ещё одним столбцом содержащим математическое ожидание значений каждой из строк. Выбираются те варианты, в строках которых стоит наибольшее значение eir этого столбца.
дополняется ещё одним столбцом содержащим математическое ожидание значений каждой из строк. Выбираются те варианты, в строках которых стоит наибольшее значение eir этого столбца.
При этом предполагается, что ситуация, в которой принимается решение, характеризуется следующими обстоятельствами:
1) Вероятности появления состояния Fj известны и не зависят от времени.
2) Решение реализуется (теоретически) бесконечно много раз.
3) Для малого числа реализаций решения допускается некоторый риск.
При достаточно большом количестве реализаций среднее значение постепенно стабилизируется. Поэтому при полной (бесконечной) реализации какой-либо риск практически исключён.
Т.о. критерий Байеса-Лапласа (B-L-критерий) более оптимистичен, чем минимаксный критерий, однако он предполагает большую информированность и достаточно длительную реализацию.
Пример 2. Определить оптимальные варианты из множества решений, заданных матрицей решений с использованием критерия Байеса-Лапласа ZBL при равновесных состояниях.
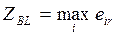
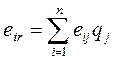
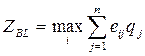
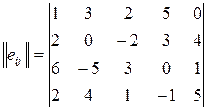
Так как состояния равновесные то, q1=q2=q3=q4=q5 q/5 =0.2
Каждый элемент матрицы умножаем на вероятность события q, которая в этой задаче равна 0.2 , после этого полученные значения складываются построчно и записываются в дополнительный столбец.
Вычисление:
ei1=1*0.2+3*0.2+2*0.2+5*0.2+0*0.2=2.2
ei2=2*0.2+0*0.2+(-2)*0.2+3*0.2+4*0.2=1.4
ei3=6*0.2+(-5)*0.2+3*0.2+0*0.2+1*0.2=1.0
ei4=2*0.2+4*0.2+1*0.2+(-1)*0.2+5*0.2=2.2
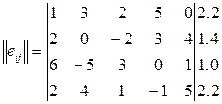
Из дополнительного столбца выбирается максимальное (max) значение – это и есть ответ.
Ответ: 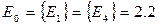
Пример 3. Определить оптимальные варианты из множества решений, заданных матрицей решений с использованием критерия Байеса-Лапласа ZBL при следующем распределении вероятностей состояния системы принятия решений: q1=0.3, q2=0.3, q3=0.2, q4=0.1, q5=0.1
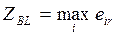
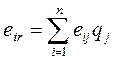
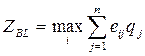
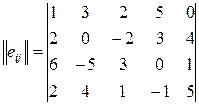
Считается точно так же как и в предыдущей задаче:
уже заданную вероятность q1 умножаем на первый элемент первой строки,
уже заданную вероятность q2 умножаем на второй элемент первой строки,
уже заданную вероятность q3 умножаем на третий элемент первой строки,
уже заданную вероятность q4 умножаем на четвёртый элемент первой строки,
уже заданную вероятность q5 умножаем на пятый элемент первой строки,
полученные ответы складываются и записываются в дополнительный столбец.
Далее то же самое проделывается с каждой строкой.
Вычисление:
ei1=1*0.3+3*0.3+2*0.2+5*0.1+0*0.1=2.1
ei2=2*0.3+0*0.3+(-2)*0.2+3*0.1+4*0.1=0.9
ei3=6*0.3+(-5)*0.3+3*0.2+0*0.1+1*0.1=1.0
ei4=2*0.3+4*0.3+1*0.2+(-1)*0.1+5*0.1=2.4
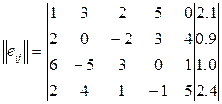
Из дополнительного (посчитанного) столбца выбирается максимальное значение (max) – это и есть ответ.
Ответ: 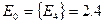
Критерий Сэвиджа
Введем вспомогательную матрицу с элементами aij : aij = max i eij − eij . Величину aij можно трактовать как максимальный дополнительный выигрыш, который достигается, если в состоянии Πj вместо варианта Pi выбирать другой, оптимальный для этого внешнего состояния вариант. Величину aij можно интерпретировать и как потери (штрафы) возникающие в состоянии Πj при замене оптимального для него варианта на вариант Pi . Тогда величина 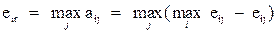 представляет собой максимально возможные (по всем внешним состояниям Πj , j = 1, n) потери в случае выбора варианта Pi . Соответствующее критерию Сэвиджа правило выбора теперь трактуется так:
представляет собой максимально возможные (по всем внешним состояниям Πj , j = 1, n) потери в случае выбора варианта Pi . Соответствующее критерию Сэвиджа правило выбора теперь трактуется так:
- каждый элемент матрицы решений вычитается из наибольшего результата max i eij соответствующего столбца.
- разности aij образуют матрицу остатков. Эта матрица пополняется столбцом наибольших разностей eir. Выбирают те варианты, в строках которых стоит наименьшее для этого столбца значение. Требования, предъявляемые к ситуации, в которой принимается решение, совпадают с требованием к ММ-критерию.
Пример и выводы. Из требований, предъявляемых к рассмотренным критериям, становится ясно, что вследствие их жёстких исходных позиций они применимы только для идеализированных практических решений. В случае, когда возможна слишком сильная идеализация, можно применять одновременно поочерёдно различные критерии. После этого среди нескольких вариантов ЛПР (лицо принимающее решение) волевым методом выбирает окончательное решение. Такой подход позволяет, во-первых, лучше проникнуть во все внутренние связи проблемы принятия решений и, во-вторых, ослабляет влияние субъективного фактора.
В соответствии с минимаксным критерием, если требуется в любых условиях избежать большого риска, то оптимальным будет то решение, для которого риск, максимальный при различных вариантах условий, окажется минимальным.
При использовании критерия Сэвиджа обеспечивается наименьшее значение максимальной величины риска:
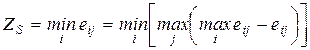
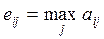
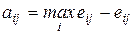
Критерий Сэвиджа, как и критерий Вальда, - это критерий крайнего пессимизма, но только пессимизм здесь проявляется в том, что минимизируется максимальная потеря в выигрыше по сравнению с тем, чего можно было бы достичь в данных условиях.
Пример 4. Определить оптимальные варианты из множества решений, заданных матрицей решений с использованием критерия Сэвиджа 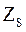
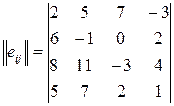
а.) Из столбца выбирается элемент с максимальным значением (max), далее из него вычитается первый элемент столбца, потом второй, потом третий, потом четвёртый.
б.) То же самое проделывается с каждым столбцом исходной матрицы.
в.) Полученные числа в том же порядке записываются в новую матрицу.
| 8-2=6 | 11-5=6 | 7-7=0 | 4+3=7 |
| 8-6=2 | 11-(-1)=12 | 7-0=7 | 4-2=2 |
| 8-8=0 | 11-1=10 | 7-(-3)=10 | 4-4=0 |
| 8-5=3 | 11-7=4 | 7-2=5 | 4-1=3 |
г.) Из каждой строки новой матрицы выбираем максимальный элемент (max) и заносим его в дополнительный столбец, дальше из этого столбца выбираем минимальный элемент (min) – это и есть ответ
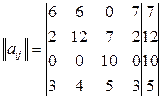
Ответ: 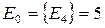
Дата добавления: 2019-04-03; просмотров: 5639;
