Критерий Ходжа-Лемана
Критерий основан на минимаксном критерии и критерии Байеса — Лапласа, характеризуется тем, что с помощью параметра выражает степень доверия к используемому распределению вероятностей. При V = 1 критерий переходит в критерий Байеса — Лапласа, а при V = 0 — в минимаксный критерий. Ситуация, в которой рекомендовано применение этого критерия, характеризуется следующими условиями: вероятности появления состояний 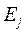 неизвестны, но некоторые предположения о распределениях вероятностей возможны; принятое решение теоретически допускает бесконечно много реализаций: при малых числах реализации допускается некоторый риск.
неизвестны, но некоторые предположения о распределениях вероятностей возможны; принятое решение теоретически допускает бесконечно много реализаций: при малых числах реализации допускается некоторый риск.
Пример 5. Определить оптимальные варианты из множества решений, заданных матрицей решений с использованием критерия Ходжа-Лемана 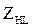 , если вероятности состояния системы принятия решений неизвестны. При решении задачи учесть, что степень доверия к позиции крайней осторожности
, если вероятности состояния системы принятия решений неизвестны. При решении задачи учесть, что степень доверия к позиции крайней осторожности 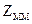 на процесс принятия решения должна быть не более 0,4.
на процесс принятия решения должна быть не более 0,4.
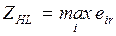
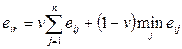
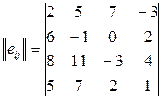
По условию 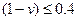 - это степень доверия к позиции крайней осторожности ZMM, или вероятность (коэффициент) возникновения минимаксного критерия, описанного в первой задаче ZMM.
- это степень доверия к позиции крайней осторожности ZMM, или вероятность (коэффициент) возникновения минимаксного критерия, описанного в первой задаче ZMM.
Возьмем 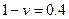 , тогда
, тогда 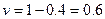 - это степень доверия к позиции критерия Байеса-Лапласа ZBL, описанного во второй третьей задаче.
- это степень доверия к позиции критерия Байеса-Лапласа ZBL, описанного во второй третьей задаче.
Критерий Ходжа-Лемана ZHL можно представить в виде:
ZHL= ZBL+ ZMM, а в этой задаче с коэффициентами, ZHL= vZBL+ (1-v)ZMM
Далее, по условию, вероятности состояния системы принятия решений неизвестны, т.е. по заданной матрице видно: вероятностей четыре (четыре строки), тогда предположим, что вероятности равноценны. Известно, что сумма всех возможных вероятностей равна 1.
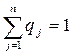 →
→ 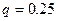
Решение (считается построчно):
а.) Каждый элемент строки умножается на вероятность 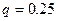
б.) Всё складывается и умножается на 0.6
г.) К полученным значениям прибавляется произведение минимального элемента строки на коэффициент 0,4
Вычисление:
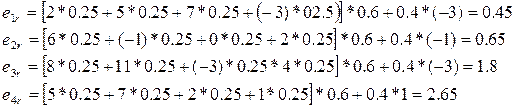
д.) Выбирается максимальное значение дополнительного столбца (max) – это и есть ответ.
Ответ: 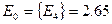
Критерий Гурвица
Стараясь занять наиболее уравновешенную позицию, Гурвиц предположил оценочную функцию, которая находится где-то между точкой зрения крайнего оптимизма и крайнего пессимизма:
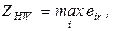
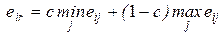
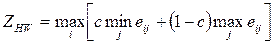
где С — весовой множитель.
Правило выбора согласно критерию Гурвица, формируется следующим образом: Матрица решений дополняется столбцом, содержащим среднее взвешенное наи- меньшего и наибольшего результатов для каждой строки. Выбираются только те варианты, в строках которых стоят наибольшие элементы eir этого столбца. При C = 1 критерий Гурвица превращается в ММ-критерий.
При C = 0 он превращается в критерий “азартного игрока”, то есть делает ставку на то, что «выпадет» наивыгоднейший случай. В технических приложениях сложно выбрать весовой множи- тель C, т.к. трудно найти количественную характеристику для тех долей оптимизма и пессимизма, которые присутствуют при принятии решения. Поэтому чаще всего пола- гают C = 1 2 .
Критерий Гурвица применяется в случае, когда :
1) О вероятностях появления состояния Πj ничего не известно.
2) С появлением состояния Πj необходимо считаться.
3) Реализуется только малое количество решений.
4) Допускается некоторый риск.
Пример 6. Определить оптимальные варианты из множества решений, заданных матрицей решений с использованием критерия Гурвица ZHW. При решении задачи учесть, что степень доверия к позиции крайней осторожности ZMM должна быть не более 0.3.
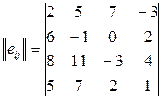
По условию 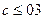 - это степень доверия к позиции крайней осторожности ZMM, или вероятность (коэффициент) возникновения минимаксного критерия, описанного в первой задаче ZMM.
- это степень доверия к позиции крайней осторожности ZMM, или вероятность (коэффициент) возникновения минимаксного критерия, описанного в первой задаче ZMM.
Возьмем 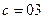 , тогда
, тогда 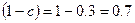 - это степень доверия к позиции критерия азартного игрока ZAG
- это степень доверия к позиции критерия азартного игрока ZAG 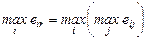
Критерий Гурвица ZHW можно представить в виде:
ZHW= ZMM+ ZAG, а в этой задаче с коэффициентами ZHW= cZMM+ (1-c)ZAG
Решение (считается построчно):
а.) Минимальный (min) элемент строки умножается на 0.3 а максимальный элемент строки умножается на 0.7
б.) Результаты умножений складываются и записываются в дополнительный столбец
Вычисление:
e1r=(-3)*0.3+7*0.7=4
e2r=(-1)*0.3+6*0.7=3.9
e3r=(-3)*0.3+11*0.7=6.8
e4r=1*0.3+7*0.7=5.2
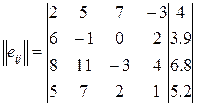
г.) Выбирается максимальное значение дополнительного столбца (max) – это и есть ответ.
Ответ: 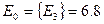
Критерий Гермейера
Отправляясь от подхода Гермейера к отысканию эффективных и пригодных к компромиссу решений в области полиоптимизации – т.е. всех решений, которые не считаются заведомо худшими, чем другие, – можно предположить еще один критерий, обладающий в некотором отношении определенной эластичностью. Он с самого начала ориентирован на величины потерь, т.е. на отрицательные значения 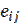 .
.
В качестве оценочной функции выступает
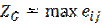
Поскольку в хозяйственных задачах преимущественно имеют дело с ценами и затратами, условие 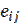 <0 обычно выполняется. В случае же, когда среди величин
<0 обычно выполняется. В случае же, когда среди величин 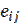 встречаются и положительные значения, можно перейти к строго отрицательным значениям с помощью преобразования
встречаются и положительные значения, можно перейти к строго отрицательным значениям с помощью преобразования 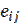 - а при подходящим образом подобранном
- а при подходящим образом подобранном 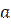 >0.
>0.
Правило выбора согласно критерию Гермейера формулируется следующим образом:
Матрица решений дополняется еще одним столбцом, содержащим в каждой строке наименьшее произведение имеющегося в ней результата на вероятность соответствующего состояния  . Выбираются те решения
. Выбираются те решения 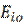 , в строках которых находится наибольшее значение
, в строках которых находится наибольшее значение 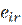 этого столбца.
этого столбца.
Пример 7. Определить оптимальные варианты из множества решений, заданных матрицей решений с использованием критерия Гермейера 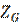 при вероятности состояния системы принятия решений:
при вероятности состояния системы принятия решений: 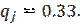
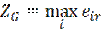
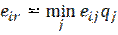
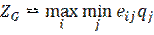
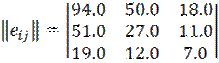
При использовании критерия Гермейера 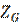 для расчёта должна получиться матрица, в которой все элементы имеют отрицательное значение.
для расчёта должна получиться матрица, в которой все элементы имеют отрицательное значение.
В исходной матрице максимум это 94, поэтому из каждого элемента вычитается любое большее число, например, 95.
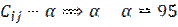
Получается матрица остатков:
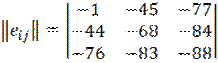
Уже заданную вероятность 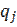 умножаем элементы матрицы.
умножаем элементы матрицы.
Вычисление:
| 
| 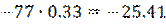
|
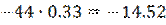
| 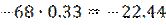
| 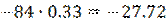
|
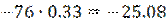
| 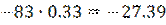
| 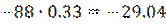
|
Полученные ответы сравниваются, из них выбираются минимальные значения, которые записываются в дополнительный столбец матрицы остатков.
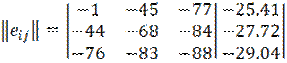
Из дополнительного столбца выбирается максимальное (max) значение – это и есть ответ.


Ответ: 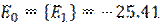 .
.
Пример 8. Определить оптимальные варианты из множества решений, заданных матрицей решений с использованием критерия Гермейера ZG при следующем распределении вероятностей состояния системы принятия решений: q1=0.3, q2=0.25, q3=0.25, q4=0.2
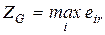
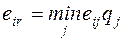

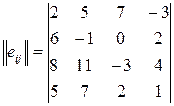
При использовании критерия Гермейера ZG для расчёта должна получится матрица, в которой все элементы имеют отрицательное значение.
В исходной матрице максимум это 11, поэтому из каждого элемента вычитается любое большее число, например, 12.
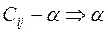
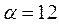
Получается матрица остатков
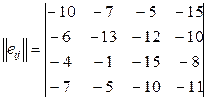
Далее вероятности q1=0.3 умножаем на числа 1 столбца, q2=0.25 умножаем на числа 2 столбца, q3=0.25 на 3 столбец и q4=0.2 на 4 столбец.
Вычисление:
| -10*03= -3 | -7*0,25= -1,75 | -5*0,25= -1,25 | -15*0,2= -3 |
| -6*0,3= -1,8 | -13*0,25= - 3,25 | -12*0,25= -3 | -10*0,2= -5 |
| -4*0,3= -1,2 | -1*0,25= -0,25 | -15*0,25= -3,75 | -8*0,2= -4 |
| -7*0,3= -2,1 | -5*0,25= -1,25 | -10*0,25= -2,5 | -11*0,2= -2,2 |
Полученные ответы сравниваются, из них выбираются минимальные значения, которые записываются в дополнительный столбец матрицы остатков.

Из дополнительного столбца выбирается максимальное (max) значение – это и есть ответ.
Ответ: 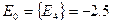
Дата добавления: 2019-04-03; просмотров: 6184;
