ВТОРОЙ 3AKОH ТЕРМОДИНАМИКИ. ЭНТРОПИЯ. ЭНЕРГИИ ГИББСА И ГЕЛЬМГОЛЬЦА. КРИТЕРИЙ САМОПРОИ3ВОЛЬНОГО ПРОТЕКАНИЯ ПРОЦЕССА

Пример 1. Один моль кислорода расширяется до десятикратного увеличения объема и одновременно охлаждается от 400К до 300К. Чему равно изменение энтропии, если для заданного
температурного интервала мольная изобарная теплоемкость кислорода C = 29,2 Дж/моль*К (С_р считаем в данном интервале температур постоянной).

Решение. Общее изменение энтропии ΔS будет складываться из изменения энтропии газа ΔS₁ при его расширении и изменения энтропии газа ΔS₂ при изменении температуры:

ΔS₁= R ln 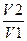, (1.3.1)

где R - газовая постоянная; V₁ и V₂ — соответственно конечный и начальный объемы газа. .Находим по формуле (1.3.1)
ΔS₁= 8,31*ln10=19,1 Дж/моль*K.

ΔS₂ =C_p*ln 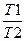, (1.3.2)

где С - мольная изобарная теплоемкость О₂; Т₂ и Т₁ — конечная и начальная температуры.
Отсюда

ΔS₂ = 29,2·1n 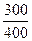= -8,05 Дж/моль*К, тогда ΔS = ΔS₁+ΔS₂= 19,1-8,05 = 11,05 Дж/моль*К.
Ответ. ΔS = 11,05 Дж/моль*К.

Пример 2. При охлаждении 12 л кислорода от 473 до 233 K одновременно повышается давление от 10⁵ до 6·10⁶. Рассчитать изменение энтропии, если мольная изобарная теплоемкость кислорода С_р = 29,2 Дж/моль*К (газ считать идеальным).

Решение. Рассчитаем число молей кислорода из уравнения состояния идеального газа

pV= nRT ; n= 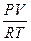=(10⁵*12*10^-3)/(8,31*473)= 0,3052 моля.

Общее изменение энтропии ΔS будет складываться из изменения энтропии ΔS₁ при увеличении давления и изменения энтропии ΔS₂ при охлаждении газа

ΔS₁ =R ln 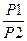, (1.З.З)

где Ρ₁ и Ρ₂ — исходное и конечное давления; R — газовая постоянная.

ΔS₂ находим по формуле (1.3.2).
Отсюда

ΔS = R ln 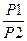+ C_pln .
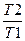Так как у нас участвует 0,3052 молей кислорода, то

ΔS =0,3052(8,31*ln(10⁵/(6*10⁶)) + 29,2*ln(233/437))=-16,77 Дж/моль*К.

(энтропия уменьшается при охлаждении газа).
Ответ. ΔS = —16,77 Дж/моль*К.

Пример 3. Определить изменение энтропии ΔS при нагревании 30 г ледяной уксусной кислоты (СН₃ СООН) от температуры плавления до 333 K. Τ_пл уксусной кислоты 289,6 K. Теплота
плавления ΔΗ_пл= 194 Дж/г, удельная теплоемкость уксусной кислоты равна 2,19 Дж/г*К.

Решение. Общее изменение энтропии Δ S Равно сумме изменения энтропии при плавлении уксусной кислоты Δ S₁ и при нагревании жидкой уксусной кислоты от Τ_пл до заданной температуры (333 К) Δ S₂

Δ S₁= Δ H_пл/T_пл (1.3.4)

1 моль СН₃СООН= 60 г.
По формуле (1.3.4) находим Δ S₁=194*30/289,6*60=20,1 Дж/К
Δ S₂ рассчитываем по формуле (1.3.2):

Δ S₂=С_pln(T₂/T₁)=2,19*30ln(333/289,6)=9,20 Дж/К.
Тогда

Δ S = Δ S₁ + Δ S₂= 20,1+9,2=29,3 Дж/К.
Ответ: Δ S = 29,3 Дж/К.

Пример 4. Определить изменение энтропии ΔS^о и энергии Гиббса ΔG^о при стандартных условиях для системы

Fe₃О₄ + CO = 3FeO + CO₂
и решить вопрос о возможности самопроизвольного протекания ее при указанных условиях.

Решение. Значения ΔS^о и ΔG^о Для реакции определяем по следствию из закона Гесса (2.2.1). Стандартные энтропии S°₂₉₈ и энергии Гиббса ΔG^о ₂₉₈ компонентов берем из табл.3.
Следовательно,
продукты реагенты

ΔS^о = ∑ ν_j S°₂₉₈ - ∑ν_i S°₂₉₈.

или

ΔS^о = 3S^о_{298 FeO} + S^о_{298 CO2} - S^о_{298 Fe3O4} - S^о_{298 CO} =3*58,79 + 213,6 -151,46 – 197,4 = 39,11Дж

продукты реагенты
ΔG^о = ∑ ν_j ΔG^о ₂₉₈ - ∑ν_i ΔG^о ₂₉₈. (1.3.6)

или
ΔG^о = 3 ΔG^о _{298 FeO} + ΔG^о _{298 CO2} - ΔG^о _{298 Fe3O4} - ΔG^о _{298 CO} = 3(-246,0) – 394,89 +1010 +137,4 = 14,51 кДж

Если ΔG < О, процесс идет самопроизвольно, при ΔG > 0 процесс не идет. В данном случае ΔG > 0, следовательно, процесс самопроизвольно не пойдет.

Ответ. ΔS° = 39,11 Дж; ΔG^о = 14,51 кДж, реакция самопроизвольно не пойдет.

Пример 5. Вычислить стандартное значение изменения свободной энергии ΔG^о реакции: C₂H₂+5/2 О₂ = 2 CО₂ + Н₂О _(ж); ΔG^о,

По табличным данным -S^о₂₉₈ и ΔΗ^о₂₉₈ для компонентов (табл. 3).

Решение. Определяем тепловой эффект и изменение энтропии реакции по закону Гесса (формулы (1.2.1) и (1.3.5)).

ΔΗ° = ΔΗ°_{298 H2O} + 2ΔΗ°_{298 CO2} - 2ΔΗ°_{298 C2H2}= -285,8+2* (-394)-226,8= -1299,6 кДж/моль;

ΔS°= S^о_{298 H2O} + 2S^о_{298 CO2} - S^о_{298 C2H2} – 5/2S^о_{298 O2} =

= 70+2213,6-200,8-2,5*205= -216,2 Дж/моль*К;
ΔS°= -0,2162 кДж/моль*К.

Изменение изобарно-изотермического потенциала находим по формуле

ΔG° = ΔΗ°- T ΔS^о, (1.3.7)

ΔG°= -1299,6+0,2162*298= -1235,19 кДж/моль.
Таким образом, ΔG^о < 0 - самопроизвольный процесс возможен.

Ответ. ΔG^о =-1235,19 кДж.

Задачи

39. Определить изменение энтропии для 1 кг воздуха при нагревании его от 223 до 323 К (при этом происходит изменение давления от 10⁶ до 10⁵ Па). Массовая теплоемкость воздуха 1,005 Дж/г*К. Средняя молекулярная масса воздуха 29.

40. Средняя массовая теплоемкость железа равна 0,486 Дж/г* К. Определить изменение энтропии ΔS при нагревании 1 кг железа от 100 до 150^оС.

41. Определить суммарное изменение энтропии при нагревании 1 моля бензола от температуры плавления (5,49 С) до полного испарения при температуре кипения (80,2^оС). Теплота
плавления бензола 126,54 Дж/г, теплота парообразования 396 Дж/г, массовая теплоемкость бензола 1,94 Дж/г* К.

42. Вычислить cyммаpное изменение энтропии при нагревании 1 моля воды от темпеpатуpы плавления до полного иcпаpения пpи температypе кипения. Теплота плавления льда 335,2 Дж/г, теплота паpообpазоваиия воды 2260 Дж/г, маccовая теплоемкость воды 4,188 Дж/г*K.

43. Вычиcлить изменение энтpопии ΔS пpи cтандapтныx
уcловияx для yравнений pеакций:

2H₂S+SO₂=2H₂O_(ж)+3S_(кр) ; Zn_(кр)+H₂SO_4(ж) = ZnSO_4(ж) + H_2(г).
CH₄ + 2O₂ = CO₂ +2H₂O_(r) .

44. Oпpеделить изменение энеpгии Гиббcа для реакции

N₂+2H₂O_(ж)=NH₄NO₂; ΔG^o

и дать заключение о возможноcти ее пpотекания пpи cтандаpтных ycловиях.

45. Вычиcлить изобарно-изотeрмичecкий потеициал ΔG^o реакций и дать заключение о возможноcти иx пpοтекания пpи cтандаpтныx yсловияx:

а) 3С₂H₂=C₆H₆ ; ΔG^o₁ ;

б) CO₂+2NH₃→NH₂-CO-NH₂ + H₂O_(ж) ; ΔG°₂;

в) СH₃-CH₂-CH₂OH→ CH₃-СН=СН₂ + Н₂О_(ж); ΔG°₃.

46. Hе пpоизводя вычиcлений, ycтанοвить знак ΔS cледyющиx пpоцеcсов:

а) 2NH_3(г)=N_2(г)+3H_2(г) ;

б) CO_2(кр)=CO_2(г) ;

в) 2NO_(г)+O_2(г)=2NO_2(г) ;

г) 2H₂S_(г)+3O_2(г)=2H₂O_(ж)+2SO_2(г) ;

д) 2CH₃OH_(г)+3O_2(г)=4H₂O_(г)+2CO_2(г).

47. Опpеделить знак изменения энтpoпии для pеакций:

2A_2(г)+B_2(г)=2A₂B­_(ж).

Возможно ли пpотекание этой pеакции в cтандаpтныχ ycловияx? Ответ обоcновать.

48. Установить, пpотекание какиx из нижеcледyющих pеакций возможно в cтандаpтных ycловияx пpи 298 K:

а) N_2(г)+1/2O_2(г) =N₂O_(г);

б) 4HCl_(г)+ O_{2 (г)} = 2Cl_{2 (г)} + 2H₂O_(ж) ;

в) Fe₂O_3(кр)+ 3CO_(г)=2Fe_(кр)+ 3CO_2(г) .

49. Вычислить ΔG для реакции:

CаCO_3(кр) = СаО_(кр)+CO_2(г)

при 298 К, 773 К и 1773 K. Зависимостью ΔH , ΔS от температуры пренебречь. Построить график зависимости ΔG от температуры и найти по графику температуру, выше которой указанная реакция может протекать самопроизвольно.

50. Вычислить ΔG°₂₉₈ следующих реакций восстановления
оксида железа (II):

а) FeO_(кр) + 1/2 C_(гр) = Fe_(кр) + 1/2 CО_{2 (г)};

б)FeO_(кр) + C_(гр) = Fe_(кр) + CO_(г) ;

в) FeO_(кр) + CO_(г) = Fe_(кр) + CO_2(г) .

Протекание какой из этих реакций наиболее вероятно?

51. Указать, какие из реакций образования оксидов азота,
и при каких температурах (высоких или низких) могут протекать самопроизвольно:

а) 2N _2(г) + O_{2 (г)} = 2N₂O_(г) ; Δ H^о₂₉₈>0 ;

б) N_2(г) + O_2(г) = 2NO_(г) ; Δ H^о₂₉₈>0 ;

в) 2NO_(г) + O_2(г) = 2NO_2(кр); Δ H^о₂₉₈<0 ;

г) NO_(г) + NO_2(г) = N₂ O_{3 (кр)} ; Δ H^о₂₉₈<0 ;

д) N_2(г) + 2O_2(г) = 2NО_2(г) ; Δ H^о₂₉₈>0 ;

52. На основании расчета ΔG°₂₉₈ реакций сделайте вывод,
какие из перечисленных ниже окислов могут быть восстановлены алюминием при 298 К: CаО; FеO; СuО, PbO; Fe₂O₃ ; Cr₂O₃?

53. Можно ли получить пероксид водорода H₂О₂ по реакции:

2H₂O_(ж) + O_{2 (г)} = 2N₂O_2(ж).

54. Возможно ли горение кальция в атмоофере оксида углерода по реакции

Са _(кр) + CО_(г) = CаO_(кр) + C_(кр).

55. Чему равно изменение энтропии Δ S при плавлении одного моля льда при 273,15 K, если изменение энтальпии при плавлении льда Δ H_пл= 6016,8 Дж/моль.