Наведенная корреляция.

В некоторых случаях высокие значения коэффициента корреляции между переменными не отражают связь между ними, а возникают вследствие преобразования результатов каких-либо измерений. То есть некоторые независимые случайные величины, полученные путем измерений, имеют нулевую корреляцию, однако некоторые операции над переменными могут привести к возникновению корреляции между ними, хотя как уже было сказано никакой корреляции (или никакого линейного соотношения) между этими переменными не существует. В книге Дж.С.Девиса “Статистический анализ данных в геологии” приводится следующий пример, описанный ниже. Предположим, что образцы гальки случайным образом выбираются на галечном пляже и без перемещения гальки измеряются ортогональные оси (X,Y,Z). Никаких попыток измерить самую длинную ось или самую короткую не предпринимается, измерения проводятся на гальках в том положении, в каком они лежат на пляже. Можно предположить, что результаты измерения по осям будут слабо коррелированы, так как измерения ортогональных осей на больших гальках будут иметь большие значения, по всем трем осям, а на маленьких гальках наоборот измерения будут иметь маленькие значения по всем трем ортогональным осям. В таблице 100 приведены замеры галек и на рисунке 100 показан корреляционный график.

Таблица 100

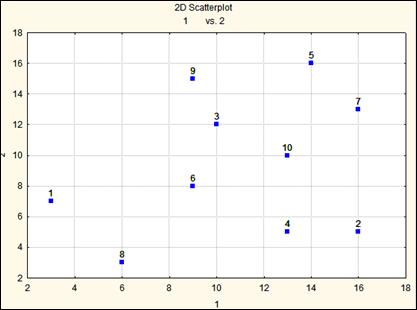
Рис. Слабая корреляция между измерениями первой и второй ортогональных осей. Корреляция равна 0.279.

Однако если изменить положение гальки согласно предварительному соглашению, по которому длинную ось гальки нужно расположить по ортогональной оси X, а короткую ось по ортогональной оси Y, то такое упорядочение приведет к изменению значений измерений и приведет к изменению корреляций. Эти изменения отражены в таблице 100 и на рисунке 100, причем эти изменения могут и не привести к изменению суммы первоначальных измерений размеров галек.

Таблица 100

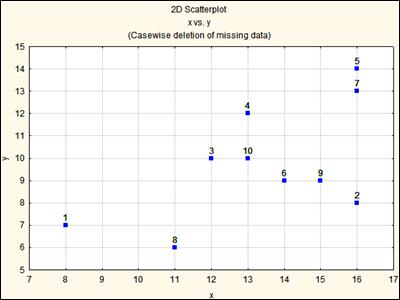
Рис. Корреляция между измерениями первой и второй ортогональных осей (X и Y) равна 0.596.

Анализ рисунка 100 свидетельствует, что упорядочение в измерениях размеров гальки привело к смещению точек на корреляционном графике к нижнему сектору диаграммы, разделенной прямой под углом 45⁰.

Наведенные корреляции, которые причиняют наибольшие беспокойства - это ложные отрицательные корреляции, которые появляются в замкнутых множествах данных. Замкнутым множеством данных называют множество данных, в котором сумма всех переменных равна 100% или 1, что означает, что переменные представляют собой определенные пропорции от целого. Так как сумма переменных есть фиксированное число, то увеличение доли одной переменной приводит к сокращению доли других переменных. В открытом множестве, в котором измерения не представляются в виде пропорций двух независимых переменных, не будет существовать корреляции. Если же открытое множество данных замкнуть преобразованием измерений в пропорции, то появятся отрицательные корреляции, хотя исходные данные первоначально представляли собой независимые переменные. Такие преобразования первоначально первоначальных данных характерны при нанесении данных на треугольные диаграммы, например трехфазные компонентные диаграммы.

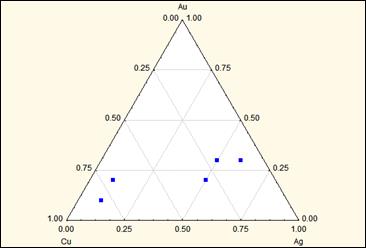
Рис. Пример треугольной диаграммы.

Эти отрицательные корреляции возникают из того факта, что по мере увеличения пропорций одного компонента, остальные два компонента – их значения должны уменьшаться. Так как таких примеров анализа по треугольным диаграммам очень много, то было предпринято много попыток правильно определять в таких данных статистические корреляционные связи, и в настоящее время нет вполне удовлетворительного метода вычисления силы связи между переменными в замкнутых множествах данных. В некоторых случаях в замкнутых таблицах для трех переменных корреляции оцениваются через дисперсии по формуле –

r_1-2 =S²₃ – (S²₁+S²₂)/2S₁*S₂