Аналитический способ расчета плоских статически определимых ферм на неподвижную нагрузку

Задачей расчета является определение опорных реакций и усилий в стержнях фермы. Напомним, что силы к ферме должны быть приложены в узлах. В этом случае стержни работают исключительно на продольные усилия. Расчет фермы следует начинать с определения опорных реакций.

Порядок определения опорных реакций рассмотрим на примере треугольной стропильной фермы (рис. 3.35).

Наклонный груз Р_I разложим на составляющие

P_X = Р_I ·Cos α; (3.24)

P_Y = Р_I ·Sin α. (3.25)

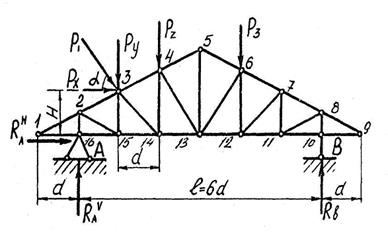
Рис. 3.35. Плоская статически определимая ферма с неподвижной

системой внешних сил

Левая опорная реакция R_А^V имеет две составляющих: вертикальную R_А^V и горизонтальную R_А^H. Для определения первой составляющей составим уравнение равновесия моментов всех сил, приложенных к ферме, относительно точки В. ∑М_В = 0;

R_А^V · L + P_X · H - P_Y · 5d - P₂ ·4d - P₃ 2d = 0.

Отсюда R_А^V = (- P_X · H + P_Y · 5d + P₂ ·4d + P₃ · 2d)/L. (3.26)

Вторая составляющая определится из уравнения проекции всех сил на горизонтальную ось X

∑X = 0 ; R_А^H + P_X = 0;

R_А^H = - P_X = - P₁·Cos α.

Если в результате вычислений окажется, что правая часть уравнения (3.26) имеет знак минус, то в действительности составляющая опорной реакции направлена в противоположную сторону против принятой в расчетной схеме (рис. 3.35). Это следует иметь в виду при дальнейших расчетах как по определению опорных реакций, так и усилий в стержнях.

Опорная реакция R_В имеет только одну составляющую - вертикальную. Величину R_В найдем, составив и решив уравнение:

∑М_А = 0.

После определения величин опорных реакций необходимо проверить правильность вычислений с помощью уравнений

∑Х = 0; ∑Y = 0.

Рассмотрим порядок определения усилий в стержнях на примере фермы с ломаным верхним поясом (рис. 3.36).

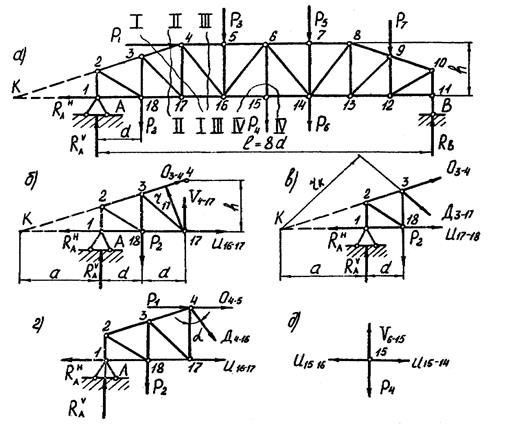
Рис. 3.36. Расчет усилий в стержнях фермы от неподвижной заданной нагрузки

Прежде чем приступить непосредственно к определению усилий в стержнях, необходимо проверить ферму на неизменяемость и статическую определимость, а также вычислить опорные реакции.

Усилия в стержнях фермы определяют методом «сечений». При этом рекомендуется определять усилия в каждом стержне независимо от ранее найденных величин усилий в других стержнях, что позволяет избежать нарастания возможных ошибок при расчетах.

При использовании метода «вырезанием узлов» ошибка в расчетах предыдущего стержня автоматически будет переходить в последующие стержни.

Порядок расчетов по методу сечений:

а) разрезаем ферму; разрез должен проходить не более чем через три стержня, в том числе и через стержень, усилие в котором требуется определить;

б) отбрасываем часть фермы (к которой приложено больше нагрузок);

в) заменяем действие отброшенной части фермы усилиями в разрезанных стержнях; при этом полагаем, что усилия в стержнях растягивающие, т.е. направленные от узла;

г) составляем такое уравнение статики, чтобы только искомое усилие входило в него в качестве единственного неизвестного;

д) решаем уравнение и находим искомое усилие; если результат будет со знаком плюс, то стержень действительно растянут, если со знаком минус, то стержень сжат.

Рассмотрим метод на примере фермы (рис. 3.36). Ферма статически определима и геометрически неизменяема. Индексы стержня и усилия в нем примем одинаковыми, например, O_3-4 - это усилие в стержне O_3-4 .

Требуется от заданной нагрузки определить величины усилий

O_3-4; U_16-17; D_3-17; D_4-16; V_4-17; V_6-15.

Усилие O_3-4 . Проведем разрез I-I, он проходит через три стержня, включая стержень O_3-4 (рис. 3.36 а). Отбросим правую часть фермы, заменив ее действие усилиями в разрезанных стержнях O_3-4 , V_4-17, U_16-17 , предполагая, что они растягивающие (рис. 3. 36 б). Эти усилия неизвестны. Рассмотрим равновесие левой части фермы. Уравнение равновесия нужно составить так, чтобы в него вошло неизвестное усилие O_3-4, но не вошли усилия V_4-17 U_{16-17 .} Очевидно, этому условию удовлетворяет уравнение - сумма моментов всех сил, приложенных к левой части фермы, относительно точки 17, находящейся на пересечении стержней V_4-17 и U_16-17.

М₁₇ = 0.

Получим (величины R_А^V и R_А^H предварительно определены)

O_3-4· r₁₇ + R_А^V· 2d - P₂ · d = 0.

Отсюда

O_3-4 = (P₂ · d - R_А^V· 2d)/ r₁₇.

Если в результате вычислений получили, что правая часть уравнения отрицатель­ная, то это значит, что стержень O_3-4 в действительности не растянут (как предположили в расчетной схеме), а сжат.

При определении усилий в стержнях фермы иногда приходится пользоваться величинами ранее найденных усилий в других стержнях. В этом случае рекомендуется сохранить принятую расчетную схему неизменной, в которой усилия в разрезанных стержнях показаны растягивающими. И только в вычислениях учитывать действительный знак величины ранее найденного усилия. Если стержень в действительности сжат, а не растянут, то при вы­числениях величина усилия встержне должна фигурировать со зна­ком минус. Если мы откорректируем расчетную схему, поменяв нап­равление действий усилия в сжатом стержне на противоположное принятому, то возможна путаница со знаками величин в дальнейших расчетах.

Усилие U_16-17. Для определения U_16-17 воспользуемся тем жеразрезом I-I (рис. 3.36 а). Величину и знак усилия опреде­лим из уравнения

∑М₄ = 0.

Получим - U_16-17 ·h + R_А^V· 2d + R_А^H·h - P₂ · d = 0.

U_16-17 = (R_А^V· 2d + R_А^H·h - P₂ · d)/h. (3.28)

Стержень растянут.

Усилие V_4-17 . Величину и знак усилия определим из уравнения ∑М_К = 0.

Моментная точка «К» находится на пересечении стержней O_3-4 и U_16-17 за пределами фермы.

Получим - V_4-17· ( а + 2d) - R_А^V· а + P₂ · (а + d) = 0.

V_4-17 = [P₂ · (а + d) - R_А^V· а]/ ( а + 2d). (3.29)

Знак усилия V_4-17 определится по результатам вычислений.

Усилие D_3-17. Проводим разрез II- II, проходящий через стержень D_3-17 и два других стержня (рис. 2.36 а). Отбросим правую часть фермы, заменим опять действие отброшенной части усилиями в разрезанных стержнях и рассмотрим равновесие оставшейся левой части фермы (рис. 2.36 в).

Величину и знак усилия определим из уравнения ∑М_К = 0.

Получим D_3-17 · r_К - R_А^V· а + Р₂ · (а + d) = 0.

D_3-17 = [R_А^V· а - Р₂ · (а + d)]/ r_К. (3.30)

Усилие D_4-16. Проводим разрез III-III (рис. 2.36 а), отбросим правую часть фермы и рассмотрим равновесие левой. Величину и знак усилия определим из уравнения равновесия - сумма проекций всех сил, приложенных к рассматриваемой части фермы, на вертикальную ось Y (рис. 2.36 г), равна нулю: ∑Y = 0.

Получим: - D_4-16 · Cos α + R_А^V - P₂ = 0;

D_4-16 = (R_А^V - P₂)/ Cos α. (3.31)

Усилие V_6-15. Проводим разрез IV-IV, начинающийся и окан­чивающийся с одной стороны фермы, т.е. вырезаем узел 15 (рис. 3.36 а). Рассмотрим равновесие вырезанного узла (рис.2.36 д). Величину и знак усилия определим из уравнения

∑Y = 0.

Получим + V_6-15 - P₄ = 0; V_6-15 = P₄. (3.32)

Стержень растянут.

Нетрудно видеть, что если бы к узлу 15 не была приложена сила P₄ , усилие

V_6-15 равнялось бы нулю. Такие стержни, работающие исключительно на местную нагрузку, представляют особую группу стержней фермы (признаки таких неработающих «нулевых» стержней приведены на рис. 3.39 – 3.41.

Дополнительные сведения по определению усилий в стержнях ферм.

В некоторых случаях не удается составить уравнение, в которое входит, только одно неизвестное. Так, например, для опреде­ления усилия в средней стойке V4_-10 фермы (рис 3.37) необходимо вырезать узел 4 и определить величину усилия с помощью уравнения ∑Y = 0,

получим - V_4-10 - О_3-4 · Cos α - О_4-5 · Cos α -Р₂ = 0,

тогда V_4-10 = - (О_3-4 · Cos α + О_4-5 · Cos α +Р₂). (3.33)

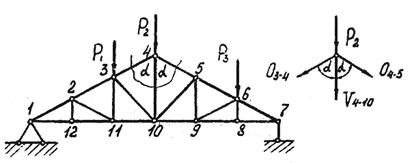
Рис. 3.37. Анализ усилий в стержнях методом вырезания узла

Очевидно, величину усилия можно определить лишь после того, как будут найдены усилия О_3-4 и О_4-5 (здесь вследствие сим­метрии О_3-4 = О_4-5 ).

Выше было указано, что разрез фермы должен проходить, как правило, не более чем через три стержня. Однако в некоторых случаях разрез может проходить и более чем через три стержня. Например, для определения усилия в стержне О_3-4 (рис. 3.38) разрез I-I через четыре стержня допустим, так как три из них пересекаются в одной точке. К этому можно добавить, что разрезать более трех стержней допустимо и тогда, когда усилия в некоторых стержнях уже определены.

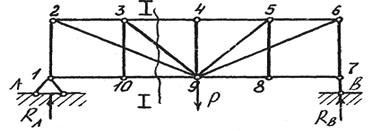Рис. 3.38. Определение усилия в стержне О_3-4 при разрезе через 4-е стержня

В фермах при заданной нагрузке некоторые стержни не работают и усилия в них, естественно, равны нулю. Перед расчетом их целесообразно отыскать, и тем самым упростить определение усилий в остальных стержнях.

Признаки неработающих, так называемых, «нулевых» стержней (рис. 3.39):

а) если в узле фермы сходятся два стержня, не лежащих на одной прямой, и к узлу не приложена нагрузка, то усилия в этих стержнях равны нулю (N₁ = N ₂ = 0) (рис. 3.39 а);

б) если в узле фермы сходятся два стержня, не лежащие на одной прямой, и к узлу приложена нагрузка Р , действующая по направлению одного из них, то усилие во втором стержне равно нулю (N ₂ = 0) (рис. 3.39 б);

в) если в узле фермы сходятся три стержня, два из которых лежат на одной прямой, и к узлу не приложена нагрузка, то усилие в третьем стержне (одиночном) равно нулю (N₃ = 0) (рис. 3.39 в).

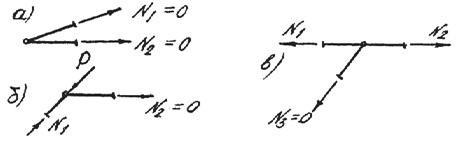
Рис. 3.39. Признаки неработающих стержней

Используем рассмотренные признаки для анализа фермы, показанной на рис. 3.40, при определении «нулевых» стержней.

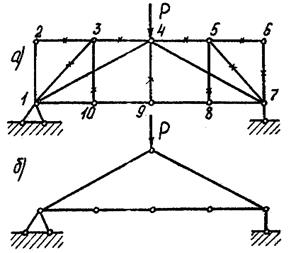
Рис. 3.40. Плоская ферма с параллельными поясами: а - исходная структура; б - упрощенная структура с удалением неработающих (нулевых) стержней

Узел 2. Усилия в обоих стержнях, сходящихся в узле, равны нулю; O_2-3 =0, V_1-2 =0.

Узел 10. Усилие в одиночном стержне равно нулю; V_3-10 =0.

Узел 9. Усилие в одиночном стержне равно нулю V_4-9 =0.

Узел 3. Если V_3-10 =0, то это равнозначно, что стержень 3-10 отсутствует. Следовательно, стержень 1-3 оказывается одиночным и усилие в нем равно нулю: D_1-3 = 0.

Узел 3. Если из четырех стержней, сходящихся в узле, в трех усилия равны нулю, то и в четвертом усилие равно нулю; O_3-4 =0.

На рис. 3.40 а двойным штрихом показаны неработающие стержни фермы.

Таким образом, из всей фермы при данной нагрузке работают только стержни, показанные на рис. 2.40 б.

Предлагается самостоятельно определить «нулевые» стержни в фермах, показанных на рис. 3.41.

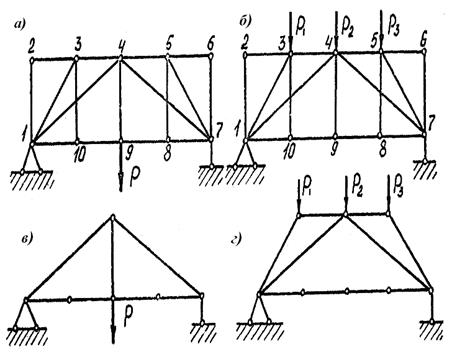
Рис. 3.41. Примеры ферм для выявления неработающих стержней: а, б – схемы ферм; в, г – работающие стержни (нулевые условно удалены)