Трехшарнирные арочные фермы
Некоторые типы конструкций трехшарнирных арочных ферм представлены на рис. 3.42. В фермах этого типа шарниров в действительности не три, как мы видим, а гораздо больше. Термин «трехшарнирная» принят условно. Подразумевается при этом, что речь идет о двух опорных шарнирах А и В и среднем шарнире Св пролете. Такая конструкция предопределяет отличие трехшарнирных ферм похарактеру работы от «традиционных» ферм балочного типа.
Трехшарнирные фермы, как и трехшарнирные арки, являются распорными системами, их опорные реакции наклонны при вертикальной нагрузке. Иначе говоря, при вертикальной нагрузке опорные реакции трехшарнирных ферм имеют каквертикальные, так и горизонтальные составляющие - распоры. (Вфермах балочного типа при вертикальной нагрузке опорные реакции имеют только вертикальные составляющие).
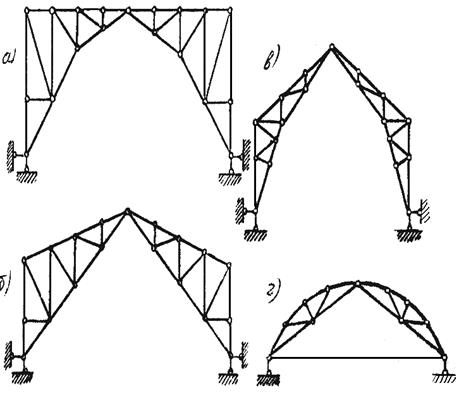
Рис. 3.42. Примеры трехшарнирных арочных ферм
Трехшарнирные фермы соединяют в себе свойства арок и ферм,. поэтому с их помощью можно перекрывать большие пролеты без возведения промежуточных опор. Они нашли широкое применение при возведении мостов, строительстве ангаров, павильонов, выставочных залов и спортивных сооружений. По внешнему виду трехшарнирные фермы легки и изящны. В некоторых сооружениях несущие металлические конструкции с использованием трехшарнирных ферм намеренно не декорируют, оставляя их открытыми для обозрения. При удачном конструктивном решении и тщательном исполнении в этих случаях трехшарнирные фермы (так же, как и арки) составляет эстетическую канву всего сооружения, придавая ему воздушность и изящество.
Определенным недостатком трехшарнирных арок является необходимость возведенияотносительно мощных и тяжелых опорных частей. Поэтому для облегчения опор, если позволяют габариты, трехшарнирные арочные фермы устраивают с затяжками (рис. 3.42 г).
Как правило, стержни трехшарнирных арочных ферм делают прямолинейными. Аналитический способ расчета трехшарнирных ферм рассмотрим на примере (рис. 3.43 а).
Предварительно проведем анализ на неизменяемость и статическую определимость. Первое необходимое условие неизменяемости как арок, так и ферм, выражается уравнением (3.23): 2У = СФ + СОП
Для арки по рис. 3.43: 2·17 = 30 + 4.
Это условие выполняется. Как известно, выполнение указанного условия является одновременно признаком статической определимости фермы. Выполнение второго необходимого условия неизменяемости в нашем случаецелесообразно установить следующим образом. В ферме (рис. 3.43 а), выделим диски - фермы простого образования АС и СВ. Совместно с диском «земля» общее количество дисков в рассматриваемой системе равно трем.Эти три диска соединяются тремя шарнирами - А, В и С (А и В - условные шарниры). Следовательно, правило соединения трех дисков в единую неизменяемую систему выполнено.
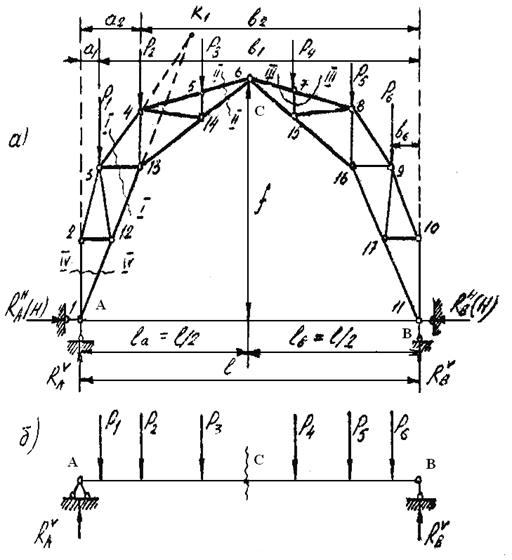
Рис. 3.43. Схема к расчету трехшарнирной арочной фермы
Делаем заключение, что ферма,представленная на рис. 3.43 а, геометрически неизменяема и статически определима.
Расчет начнем с определения опорных реакций. Для определения вертикальной составляющей левой опорной реакции RAV приравняем нулю сумму моментов всех сил, приложенных к ферме, относительно точки В ∑МВ = 0;
RAV· L - P1 · b1 - P2 · b2 - … - P6 · b6 = 0,
отсюда
RAV = (P1 · b1 + P2 · b2 + … + P6 · b6)/L = ∑МВ /L.
Приравнивая нулю сумму моментов всех сил, приложенных к ферме, относительно точки А, найдём вертикальную составляющую RBV правой опорной реакции.
RВV = (P1 · a1 + P2 · a2 + … + P6 · a6)/L = ∑МA /L = ∑МA /L.
Можно сделать проверку, приравняв нулю сумму проекций всех сил (включая теперь RAV и RВV )на вертикальную ось: ∑Y = 0.
Горизонтальную составляющую левой опорной реакции RAH найдем, используя условие, что сумма моментов всех сил, расположенных слева от среднего шарнира С, относительно этого шарнира равна нулю
RAV· Lа - Р1 (Lа - а1) - Р2 (Lа - а2) - Р3 (Lа - а3) - RAH · f = 0;
RAH = [RAV· Lа - Р1 (Lа - а1) - Р2 (Lа - а2) - Р3 (Lа - а3)] /f.
Нетрудно видеть, что числитель здесь представляет собой величину изгибающего момента для простой балки на двух опорах, того же пролета, под той же нагрузкой в сечении C под средним шарниром (рис, 3.43 б). Обозначив величину этого изгибающего момента через МС0, запишем
МС0 = RAV· Lа - Р1 (Lа - а1) - Р2 (Lа - а2) - Р3 (Lа - а3).
Тогда
RAH = МС0 / f. (3.36)
Горизонтальная составляющая правой опорной реакции RВH равна также
RВH = МС0/ f.
Следовательно, горизонтальные составляющие опорных реакций правой и левой равны по величине RAH = RВH = Н .
В статике сооружений их принято называть распором и обозначать индексом «Н».
Усилия в стержнях определяются как для обычной балочной фермы.
_Усилие_03-4. Проведем разрез I-I (рис. 3.43 а), отбросим правую часть фермы, заменим ее действие усилиями в разрезанных стержнях, полагая, что они растянуты, и рассмотрим равновесие левой части фермы (рис.3.44 а).
Моментная точка 13 находится на пересечении двух остальных разрезанных стержней. Искомое усилие О3-4 определим из уравнения
∑М13 = 0,
выражающего условие, что момент всех сил, действующих на левую часть фермы относительно моментной точки 13, равен нулю. Раскроем уравнение
О3-4· r1 + RAV·x1 - P1 · r2 - H · y1 = 0,
отсюда О3-4 = (RAV·x1 - P1 · r2 - H · y1)/r1 .
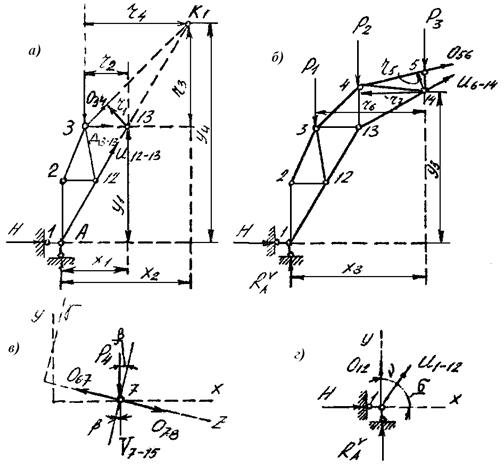
Рис. 3.44. Схема к расчету усилий в стержнях фермы
Усилие D 3-13. Воспользуемся тем же разрезом I-I. Моментная точка КI находится на пересечении стержней 3-4 и 12-13.Составляем уравнение равновесия ∑МK1 = 0
D3-13 · r3 + RAV·x2 - P1 · r4 - H · y2 = 0,
отсюда D3-13 = (RAV·x2 - P1 · r4 - H · y2) /r3.
Усилие U12-13.Воспользуемся еще раз разрезом I-I. Моментная точка 3 находится на пересечении стержней 3-4 и 3-13. Искомое усилиеопределим из уравнения ∑М3 = 0. Прежде чем записать это уравнение в развернутом виде, необходимо, как мы видели выше, найти плечи всех сил, действующих на рассматриваемую левую часть фермы, относительно моментной точки 3. На рис. 3.44 а они не показаны. Предлагается это сделать самостоятельно. Напоминаем, что плечом силы относительно выбранной моментной точки является величина перпендикуляра, опущенного из моментной точки налинию действия данной силы.
Усилие О5-6.Проведем разрез П-П (рис. 3.43 а). Отбросим правую часть фермы, заменим ее действие усилиями в разрезанных стержнях, полагая их растянутыми (направление усилий в стержнях от узлов), и рассмотрим равновесие левой части фермы (рис. 3.44 б). Искомое усилие О5-6определим из уравнения
∑М14 = 0;
О5-6 · r5 + RAV·x3 - P1 · r6 - P2 · r7 - H · y3 = 0.
Отсюда
О5-6 = (RAV·x3 - P1 · r6 - P2 · r7 - H · y3) /r5.
Усилие U6-14. Воспользуемся тем же разрезом П-П. Искомое усилие U6-14 можно определить из уравнения ∑М5 = 0.
Предлагаем составить и записать это уравнение в развернутом виде самостоятельно, предварительно определив плечи сил.
Усилие V7-15. Вырежем узел 7 (рис. 3.43 а). Рассмотрим равновесие вырезанного узла 7 (рис. 3.44 в). Искомое усилие определим из уравнения ∑γ = 0, выражающего условие, что сумма проекций усилий в стержнях фермы, сходящихся в узле 7, на ось γ, перпендикулярную линии действия усилий О6-7 и
О 7-8, равна нулю.
V7-15 · Cos β - P4 · Cos β = 0.
Отсюда V7-15 = - P4. Стержень V7-15 сжат.
Усилие U1-12. Проведем разрез IV - IV (рис. 3.43 а). Рассмотрим равновесие левой части фермы (рис. 3.44 г). Искомое усилие определится из уравнения
∑Х = 0;
+ U1-12 · Cos σ + Н = 0.
Отсюда U1-12 = - Н/ Cos σ. Стержень U1-12 сжат.
Усилие О1-2. Воспользуемся тем же разрезом IV-IV. Искомое усилие О1-2 определится из уравнения ∑Y = 0;
+ О1-2 + RAV + U1-12 · Sin σ = 0.
Отсюда О1-2 = - (RAV + U1-12 · Sin σ) = Н · tg σ - RAV.
Если величина правой части уравнения будет иметь знак минус, стержень О1-2 сжат, если знак плюс - растянут.
Подобным образом можно определить усилия во всех остальных стержнях рассмотренной трехшарнирной арки.
3.4.5. Перемещения в статически определимых фермах
Если к ферме приложить внешнюю нагрузку, то она изменит свою форму и размеры. Это происходит вследствие того, что стержни ферм упруго деформируются под действием продольных усилий. При этом растянутые стержни удлиняются, сжатые - укорачивается. Упругая деформация несущих конструкций, в том числе и ферм, под действием внешней нагрузки - это неизбежное нормальное явление. При проектировании обращают внимание на главный компонент деформации фермы под нагрузкой - прогиб (f) посредине пролета. Дело в том, что жесткость несущих конструкций, в том числе и ферм, которую оценивают показателем f / L , где L - пролет является очень важной эксплуатационной характеристикой. Для ферм разного назначения норма жесткости находится в пределах 1/300 - 1/750. Величина жесткости должна бытьоптимальной. Например, если ферма имеет малую жесткость f / L > 1/200, то она вследствие большого прогиба под нагрузкой может оказаться непригодной к использованию, даже если условия прочности выполнены.
Рассмотрим способ аналитического определения прогиба фермы (pиc.3.45). Статически определимая ферма пролетом 4 метра нагружена в узле 2 одной сосредоточенной силой Р = 10 т. Материал, из которой изготовлена ферма, - сталь, имеющая величину модуля упругости Е-=2,1·106 кг/см2. Требуется аналитически определить прогиб посредине пролета f, т.е. вертикальное перемещение узла 4. Результаты вычислений приведены в табл. 3.1.
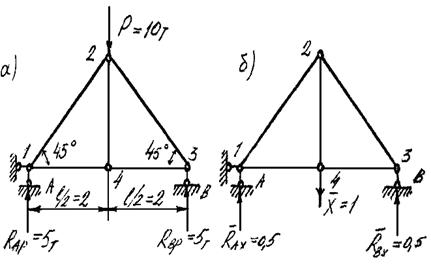
Рис. 3.45. К расчету перемещений фермы: а - схема нагружения заданной нагрузкой; б - схема нагружения фиктивной единичной нагрузкой в узле 4, премещение которого требуется определить
Перемещения узлов фермы определяются по формуле:
∆ХР = ∑ (NX · NP · Li) / (E · Fi), (3.37)
где ∆ХР - искомое перемещение, см;
NX - усилие в стержне фермы от действия фиктивной единичной силы X = 1, приложенной к ферме в искомом узле по искомому направлению; в нашем примере единичную силу прикладываем в узле 4 вертикально вниз (рис. 3.45 б).
NP - усилие в стержне фермы от заданной нагрузки, в нашем примере от
Р = 10 т ;
Li - длина i -го стержня, см;
E - модуль упругости материала фермы, в нашем случае E = 2,1· 106 кг/см2;
Fi - площадь поперечного сечения i -го стержня, см.
Приступим к расчету. Сначала определим опорные реакции и усилия в стержнях фермы от действия заданной силы Р = 10 т (рис.3.45 а).
Опорные реакции. Вследствие полной симметрии опорные реакции одинаковы и равны RAP = RBP = 5 т = 5000 кГ.
Усилие O1-2. Вырежем узел 1 и рассмотрим его равновесие (рис.3.46 а).
∑Y = 0: + RA + O1-2 · Sin α = 0.
Отсюда O1-2 = - RAP / Sin 45º = - 5000/ 0,707 = - 7072 кГ.
Вследствие симметрии O2-3 = - 7072 кГ.
Усилие U1-4P. Также используем условие равновесия узла I: ∑X = 0:
+ U1-4P + O1-2P · Cos 45º = 0.
Отсюда U1-4P = - O1-2P · Cos 45º = -( -7072) · 0,707 = + 5000 кГ.
Вследствие симметрии U3-4 = + 5000 кГ.
Усилие V2-4P. Вырежем узел 4. Рассматривая систему стержней, сходящихся в узле, можно без труда обнаружить, что стержень 2-4 подпадает под признак «нулевого». Напоминаем формулировку этого признака: если в узле сходятся три стержня, два из них расположены по одной прямой, и к узлу не приложена нагрузка, то усилие в третьем стержне равно нулю. Следовательно, усилие
V2-4P = 0.
Заметим, что величину усилия в стержне 1-2 можно установить, рассматривая равновесие узла 4, составив и решив уравнение статики: ∑Х = 0.
Определим усилия в стержнях фермы от действия единичной силы Хˉ = 1 (рис. 3.46 б).
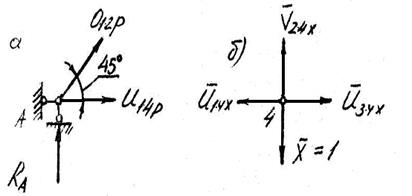
Рис. 3.46. Определение усилий в стержнях узла 1 (а) и узла 4 (б)
Значения усилий в стержнях фермы (кроме усилия V 2-4Х в стержне 2-4)от действия силы Хˉ = 1 можно определить, не прибегая к специальным расчетам, из численного отношения величин Р и Хˉ = 1. Усилие V2-4X. Вырежем и рассмотрим равновесие узла 4 (рис. 3.46 б). Так как сила
Хˉ =1 приложена к узлу 4, то стержень 2-4 в этом случае не является нулевым. Усилие в нем определим, составив и решив уравнение ∑ Y = 0 V2-4X - Хˉ = 0.
Отсюда V2-4X = + 1.
Результаты вычислений поместим в таблицу 3.1.
Таблица 3.1
Данные к расчету перемещения узла 4 от заданной нагрузки
| № стержня | Длина стержня, см | Площадь сечения, см2 | Усилие в стержне от силы Р=1 | Усилие в стержне от силы Р=10 Тс | (NX · NP · Li) / Fi |
| 1-2 | -0,707 | -7072 | |||
| 2-3 | -0,707 | -7072 | |||
| 1-4 | 0,5 | ||||
| 3-4 | 0,5 | ||||
| 2-4 |
Вычислим значения величины (NX · NP · Li) / Fi для каждого стержня и результаты поместим в правый столбец табл. 3.1 Модуль упругости E одинаков для материала всех стержней, поэтому его значение пока опустим и учтем в итоговом результате вычислений.
Подсчитаем величину искомого прогиба ∑ (NX · NP · Li) / Fi = + 241480.
Прогиб f = ∆ХР = ∑ (NX · NP · Li) / (E · Fi) = 241480 / 2100000 = 0,11 cм.
Подсчитаем величину показателя жесткости фермы
f / L = 1,1 · 10-1 / 4 · 102 = 1 / 4000 = 0, 00025.
Такая классическая методика расчета перемещений узлов ферм применима для простых ферм с небольшим количеством стержней. Для сложных ферм (статически определимых и неопределимых) при большом количестве стержней, а также объемных ферм в настоящее время используются программы расчета ферм, например, по методу конечных элементов предлагается использовать компьютерную программу 3DFerm (ОСКАЛ).
Дата добавления: 2018-03-02; просмотров: 3620;
