Глава 5. Плоские статически определимые фермы.

Элементы ферм.

Фермой называется решетчатая стержневая система, образованная из шарнирных узлов, объединенных между собой прямолинейными стержнями. Фермы загружают в узлах сосредоточенными силами, от действия которых возникают реакции опор и продольные усилия в стержнях. Силовой расчет фермы состоит в определении этих усилий.

Следует иметь в виду, что реальные фермы имеют жесткие узлы и являются статически неопределимыми. При замене жестких узлов шарнирными узлами , величины усилий в стержнях практически не меняются, но расчет значительно упрощается.

На рис.5.1 показана ферма, на примере которой установим элементы ферм. Эта ферма состоит из 10 шарнирных узлов (У=10), 17 стержней, объединяющих узлы (С=17) и двух шарнирных опор, одна из которых неподвижная. Число опорных связей равно 3 (С₀=3). Узлы А и В называют опорными. Расстояние между опорными узлами является длиной пролета фермы. Расстояние между соседними узлами по

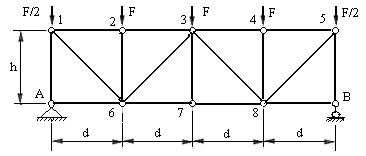
Рис.5.1

горизонтали называется длиной панели и обозначается буквой d. Расстояние между соседними узлами по вертикали называется высотой фермы и обозначается буквой h.

Стержни, ограничивающие ферму сверху, образуют верхний пояс и называются стержнями верхнего пояса.

Стержни, ограничивающие ферму снизу, образуют нижний пояс и называются стержнями нижнего пояса.

Остальные стержни образуют решетку фермы. При этом вертикальные стержни называют стойками, а наклонные – раскосами. Раскосы могут быть восходящими и нисходящими. Характер раскосов устанавливают в зависимости от их наклона, если рассматривать ферму от опор к середине. В приведенной на рис.5.1 ферме раскосы 1-6 и 5-8 являются нисходящими, а раскосы 3-6 и 3-8 восходящими. В нисходящих раскосах возникают растягивающие усилия, а в восходящих раскосах возникают сжимающие усилия.

Напомним, что фермы образуются по второму варианту и они должны удовлетворять условию неподвижности на плоскости:

2У – С – С₀ = 0

Проверим, выполняется ли это условие для фермы, представленной на рис.5.1.

2∙10 – 17 – 3 =0 , 0 = 0.