Шпренгельные фермы. Определение усилий в стержнях шпренгельных ферм.
Шпренгельные фермы состоят из простых плоских ферм, называемых основными, и дополнительных шарнирно стержневых устройств, называемых шпренгелями. Шпренгели позволяют передавать нагрузки, приложенные к стержням, на узлы основных ферм.
Если шпренгель передает приложенную к нему нагрузку на узлы загруженного пояса основной фермы, то его называют одноярусным. Если же шпренгель передает приложенную к нему нагрузку на узлы не загруженного пояса основной фермы, то его называют двухъярусным.
Рассмотрим простую ферму с параллельными поясами и раскосной решеткой, загруженную в узлах верхнего пояса силами 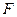 и силами
и силами 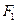 вне узлов (рис.5.25). Стержни этой фермы называют стержнями первой категории, или стержнями основной фермы.
вне узлов (рис.5.25). Стержни этой фермы называют стержнями первой категории, или стержнями основной фермы.
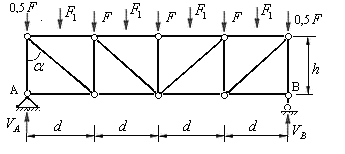
Рис.5.25
Силы 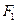 вызывают изгиб стержней верхнего пояса фермы, что не допускается в фермах. Поэтому силы
вызывают изгиб стержней верхнего пояса фермы, что не допускается в фермах. Поэтому силы 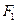 необходимо передать на смежные узлы верхнего (или нижнего) пояса фермы. Пусть силы
необходимо передать на смежные узлы верхнего (или нижнего) пояса фермы. Пусть силы 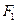 в первой и четвертой панелях фермы требуется передать на узлы верхнего пояса фермы, а во второй и третьей панелях те же силы требуется передать на узлы нижнего пояса фермы. Для этого врезают шарниры в поясные стержни и в раскосы на линиях действия сил
в первой и четвертой панелях фермы требуется передать на узлы верхнего пояса фермы, а во второй и третьей панелях те же силы требуется передать на узлы нижнего пояса фермы. Для этого врезают шарниры в поясные стержни и в раскосы на линиях действия сил 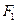 в каждой панели фермы, и эти шарниры объединяют между собой стержнями. Получают дополнительные стойки, принадлежащие шпренгелям. Затем шарниры, расположенные на раскосах основной фермы соединяют с соседними узлами верхнего или нижнего поясов. В результате получают раскосы одноярусных шпренгелей (в первой и четвертой панелях) и раскосы двухъярусных шпренгелей (во второй и третьей панелях фермы рис.5.26). Стойки и раскосы шпренгелей помечены на рис.5.26 двумя черточками. Эти стержни относятся ко второй категории шпренгельных ферм.
в каждой панели фермы, и эти шарниры объединяют между собой стержнями. Получают дополнительные стойки, принадлежащие шпренгелям. Затем шарниры, расположенные на раскосах основной фермы соединяют с соседними узлами верхнего или нижнего поясов. В результате получают раскосы одноярусных шпренгелей (в первой и четвертой панелях) и раскосы двухъярусных шпренгелей (во второй и третьей панелях фермы рис.5.26). Стойки и раскосы шпренгелей помечены на рис.5.26 двумя черточками. Эти стержни относятся ко второй категории шпренгельных ферм.
Два дополнительно введенные шарнира каждой панели фермы объединяют с соседними узлами верхнего или нижнего пояса. Эти стержни принадлежат шпренгелям, но совмещаются со стержнями основной фермы, образуя стержни третьей категории шпренгельной фермы. На рис.5.26 эти стержни показаны двойными линиями (сплошными и штриховыми).
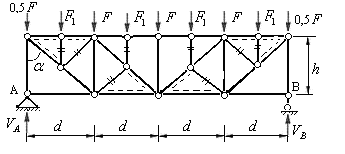
Рис.5.26
В результате получаем конструкции одноярусного (рис.5.27,а) и двухъярусного (рис.5.27,б) шпренгелей. Опорами одноярусного шпренгеля являются соседние узлы загруженного (в рассматриваемом случае верхнего) пояса фермы, а опорами двухъярусного шпренгеля являются соседние узлы незагруженного пояса фермы (нижнего).
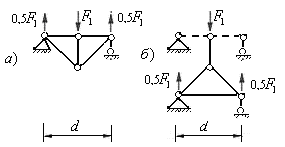
Рис.5.27
При загруженном нижнем поясе фермы, сосредоточенные силы, приложенные вне узлов, можно также передать на узлы нижнего или верхнего пояса с помощью одноярусных или двухъярусных шпренгелей. На рис.5.28 показаны конструкции таких шпренгелей.
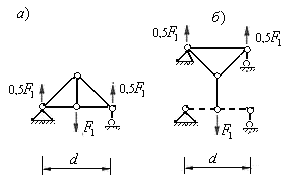
Рис.5.28
Для определения усилий в стержнях шпренгельных ферм необходимо:
1) Образовать основную ферму путем удаления всех шпренгелей и определить нагрузки, действующие на её узлы.
В узлах, на которые опирались удаленные шпренгели, следует приложить силы равные и противоположно направленные реакциям опор удаленных шпренгелей, а также заданные силы. Если принять 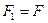 , то основная ферма при расчете шпренгельной фермы, представленной на рис. 5.26, будет иметь нагрузки, показанные на рис.5.29.
, то основная ферма при расчете шпренгельной фермы, представленной на рис. 5.26, будет иметь нагрузки, показанные на рис.5.29.
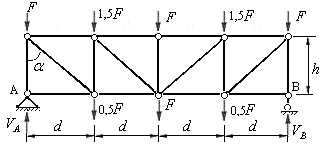
Рис.5.29
Реакции опор и усилия в стержнях основной фермы (усилия в стержнях первой категории) определяются, как и при расчете простых ферм.
2) Усилия в стержнях второй категории определяют из расчета шпренгелей по методу равновесия узлов. Если во всех панелях заданной фермы установлены однотипные шпренгели, то определяются усилия в стержнях одного из них.
3) Усилия в стержнях третьей категории равны алгебраической сумме усилий в соответствующих стержнях основной формы и шпренгелей.
Пример 5.2 Определить усилия в стержнях второй панели заданной фермы с двухъярусными шпренгелями (рис.5.30). Для расчета принять 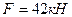 ,
, 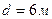 ,
, 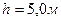 .
.
Решение: Обозначим опорные узлы фермы буквами А и В, а узлы второй панели заданной фермы – цифрами.
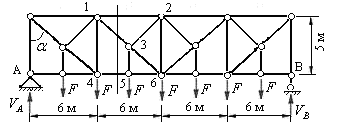
Рис.5.30
Образуем основную ферму, удалив двухъярусные шпренгели всех четырех панелей. Силы, приложенные к узлам шпренгелей, передаются на узлы верхнего пояса основной фермы. На рис.5.31 показаны силы, действующие на узлы основной фермы.
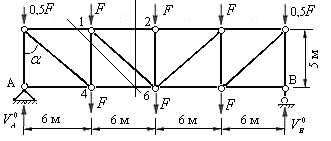
Рис.5.31
Вычисляем реакции опор основной фермы, используя условия симметрии её загружения.
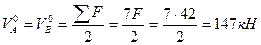
Определяем усилия в стержнях второй панели основной фермы, т.е. в стержнях 1-2, 1-6, 4-6, 1-4, и 2-6. Усилие в стойке 2-6 определяется из равновесия узла 2 и равно: 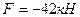 . Усилия в остальных стержнях определяем методом равновесия дисков. Рассекаем ферму сквозным вертикальным сечением на два диска, отбрасываем правый диск, а его действие на левый заменяем неизвестными усилиями в рассеченных стержнях (рис.5.32).
. Усилия в остальных стержнях определяем методом равновесия дисков. Рассекаем ферму сквозным вертикальным сечением на два диска, отбрасываем правый диск, а его действие на левый заменяем неизвестными усилиями в рассеченных стержнях (рис.5.32).
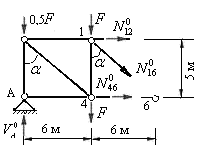
Рис.5.32
Составляем уравнения равновесия левого диска, используя следующие условия равновесия:
- (точка 1 является моментной для усилия в стержне 4-6)
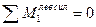

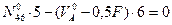

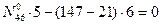

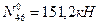
- (точка 6 является моментной для усилия в стержне 1-2)
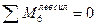

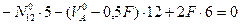

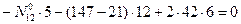

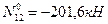
Для определения усилия 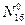 составляем уравнение равновесия, используя условие:
составляем уравнение равновесия, используя условие: 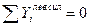

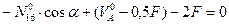

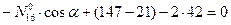

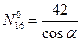
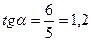

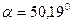

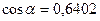 ,
, 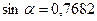 ,
,
тогда: 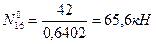
Проверяем вычисленные усилия. Для этого составляем уравнение равновесия рассматриваемого диска, используя условие равновесия:
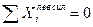

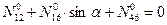

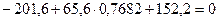

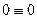 .
.
Определяем усилие в стойке 1-4 основной фермы. Для этого рассекаем ферму на 2 диска наклонным сечением, рассекающим три стержня, включая стойку 1-4.
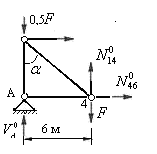
Рис.5.33
Рассматриваем левый диск (рис.5.33) и составляем уравнение равновесия, используя условие: 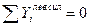

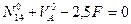

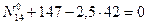

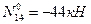
Определяем усилия в стержнях шпренгеля второй панели заданной фермы (рис.5.34,а), используя метод равновесия узлов. Из равновесия узла 5 следует, что усилие в стойке 5-3 равно силе 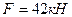 , т.е стойка 5-3 растянута.
, т.е стойка 5-3 растянута.
Для определения усилий в стержнях 1-2 и 1-3 шпренгеля вырезаем узел 1, выбираем рациональные направления осей проекций и составляем уравнения равновесия этого узла:
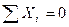

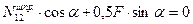

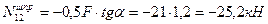
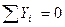

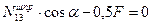

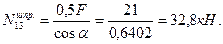
Усилие в стержне 2-3 шпренгеля равно усилию в его стержне 1-3.
Вычисляем усилия в стержнях 1-2 и 1-3 заданной фермы:
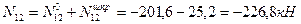
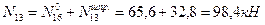
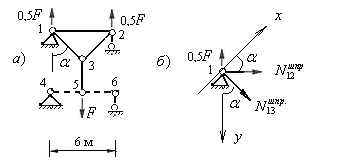
Рис.5.34
Проверим, правильно ли вычислены эти усилия. Для этого рассечем заданную ферму во второй панели так, чтобы были рассечены три стержня (рис.5.30) и рассмотрим равновесие левого диска, загруженного силами, показанными на рис.5.35.
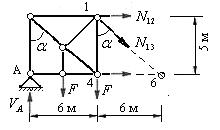
Рис.5.35
Составим два уравнения равновесия, используя условия:
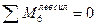

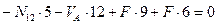

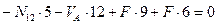

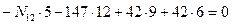

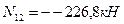
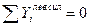

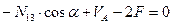

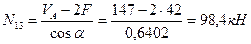
Таким образом, усилия определены правильно.
Вопросы для самоконтроля полученных знаний.
1. Что называется фермой?
2. Какие усилия появляются в элементах ферм н почему?
3. Почему фермы более экономичны по сравнению с балками?
4. Какие элементы различают в фермах?
5. По каким признакам классифицируют фермы?
6. Какие методы применяют для определения усилий в стержнях ферм?
7. Как применяется способ вырезания узлов для ручного счета? В чем достоинства и недостатки этого способа?
8. Приведите частные случаи равновесия узлов.
9. В каком случае рационально определять усилия способом моментной точки?
10. Как зависят усилия в поясах балочной фермы от ее высоты?
11. Как изменяются усилия в поясах балочной фермы вдоль ее пролета?
12. Когда удобно применять способ проекций? В чем отличие характера работы восходящих и нисходящих раскосов балочной фермы?
13. Как изменяются усилия в раскосах балочной фермы вдоль ее пролета?
14. Приведите примеры использования для расчета ферм балочных усилий.
15. В каких случаях применяется способ замкнутого сечения?
16. Как применяется способ двух сечений?
17. Что такое шпренгельная ферма?
18. С какой целью применяют шпренгели?
19. Чем отличается работа двухъярусных шпренгелей от одноярусных?
20. На какие типы делятся стержни шпренгельных ферм?
21. Каковы особенности определения усилий и построения линий влияния в шпренгельных фермах?
Дата добавления: 2019-04-03; просмотров: 7111;
