Работа внутренних усилий (потенциальная энергия стержневой системы).

При загружении плоской упругой системы внешними силами, в её поперечных сечениях возникают изгибающие моменты, продольные силы и поперечные силы. Они непрерывно меняются по длине каждого участка каждого стержня, т.е. являются функциями переменной .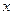

Рассмотрим упругую балку, загруженную в вертикальной плоскости произвольной силой 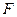, достигшей конечного значения (рис.6.2). Выделим элемент балки длиной 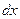, взятый на переменном расстоянии от начала участка.

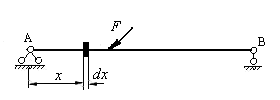
Рис.6.2

На этот элемент будут действовать внутренние усилия 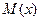, , 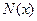, 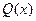показанные на рис.6.3.

Эти усилия могут рассматриваться как внешние силы, действующие на элемент длиной 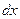упругой системы. Кроме того, они являются взаимно ортогональными, т.е. такими силами, которые совершают работу только на собственных перемещениях. Изгибающие моменты вызывают взаимные повороты смежных торцов выделенного элемента балки. Если левую грань элемента жестко закрепить (рис.6.4), то правая грань получит поворот в направлении момента 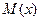на угол 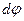, величина которого определяется по формуле, известной из сопротивления материалов:

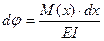
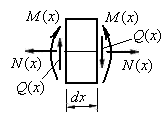
Рис.6.3

Изгибающий момент 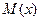совершает на этом перемещении элементарную работу, равную:

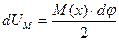, или с учетом предыдущей зависимости:

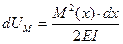(6.5)

Для вычисления полной работы, которую совершают изгибающие моменты заданной стержневой системы, необходимо выражение (6.5) проинтегрировать по всем участкам и найти алгебраическую сумму этих интегралов, т.е.:

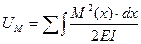(6.6)

Аналогично, продольные силы 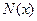вызывает продольные деформации элемента системы и совершает на этих перемещениях работу, численно равную:

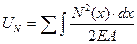(6.7)

Поперечные силы 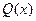вызывают взаимные сдвиги граней элемента системы в направлениях, перпендикулярных осям стержней, и совершают на этих перемещениях работу, определяемую по формуле:

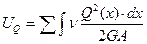(6.8)

Полная работа всех внутренних усилий (потенциальная энергия стержневой системы) определяется суммой работ, совершаемых каждым усилием, т.е.:

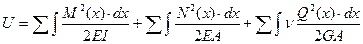(6.9)

В формуле (6.9) содержатся следующие параметры сечений стержневой системы:

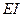- изгибная жесткость поперечных сечений стержней на отдельных участках;

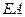- жесткость сечений стержней при их растяжении (сжатии);

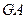- жесткость сечений стержней при сдвиге;

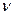- коэффициент, учитывающий неравномерность распределения касательных напряжений по высоте сечений. Его величина зависит от формы поперечного сечения.

Примечания:

1) Потенциальная энергия балочных и рамных систем вычисляется по формуле (6.6), так как влияние продольных и поперечных сил в таких системах очень мало по сравнения с влиянием изгибающих моментов;

2) Потенциальная энергия ферм, в стержнях которых возникают только продольные усилия, вычисляется по формуле (6.7).

3) Влияние поперечных сил учитывается при вычислении потенциальной энергии некоторых типов пологих арок.