Аналитический метод определения внутренних усилий в сечениях трехшарнирной арки.

Рассмотрим трехшарнирную арку, загруженную вертикальными силами (рис.4.9,а), а также балку на двух шарнирных опорах, имеющую тот же пролет и загруженную теми же силами, что и арка (рис.4.9,б). Реакции опор и распор арки определяем по формулам (4.12), (4.13) и (4.15).

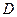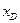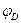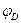Проведем нормальные сечения арки и балки с абсциссой . В сечении арки проведем касательную к оси и обозначим угол её наклона к горизонтальной прямой, через . Ордината сечения арки определяется из уравнения очертания оси арки, а тангенс угла из производной от этого уравнения по абсциссе .

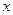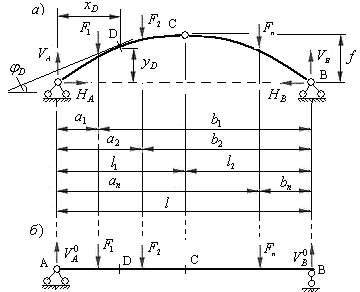
Рис.4.9

Отбросим правые отсеченные части арки и балки, а их действие на левые части, заменим внутренними усилиями в сечении. В сечении балки действуют две составляющие: поперечная сила 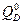и изгибающий момент 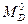(рис.4.10,б), а в сечении арки действуют три составляющие внутренних усилий: поперечная сила 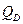, продольная сила 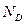и изгибающий момент 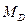(рис.4.10,а). На рис.4.10 показаны направления усилий, соответствующие их положительным знакам.

Определим балочные усилия в сечении 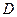, используя два условия равновесия левой отсеченной части балки (рис.4.10,б):

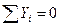
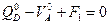откуда 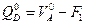(4.16)

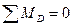
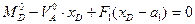_, откуда:

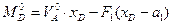(4.17)

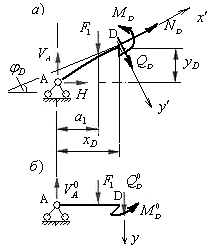
Рис.4.10

Определим арочные усилия в сечении , используя три условия равновесия левой отсеченной части арки (рис.4.10,а):

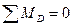
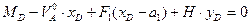
_, откуда:

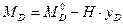(4.18)

Итак, изгибающий момент в произвольном сечении трехшарнирной арки равен разности между балочным изгибающим моментом в соответствующем сечении и произведением распора арки на ординату её оси в заданном сечении.

Изгибающий момент принимается со знаком плюс, если он растягивает нижние волокна арки, т.е. если он стремится повернуть левую отсеченную часть против часовой стрелки, а правую отсеченную часть по часовой стрелке. При противоположных направлениях действия, изгибающий момент принимается со знаком минус.

Из формулы (4.18) следует, что изгибающий момент в любом сечении арки имеет значительно меньшее значение, чем балочный изгибающий момент.

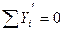
Откуда: 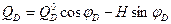(4.19)