Вычисление усилий от действия неподвижных нагрузок по линиям влияния.

Рассмотрим линию влияния некоторого усилия S на некотором участке стержневой системы. Пусть все ординаты этой линии влияния имеют знак плюс (рис.3.6,а).

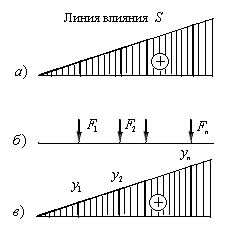
Рис.3.6

Загрузим эту линию влияния системой вертикальных сосредоточенных сил F₁,F₂….F_n, направленных вниз, т.е. в том же направлении, что и подвижный груз F=1 , от действия которого построена линия влияния (рис.3.6,б).

Обозначим ординаты линии влияния под силами буквами 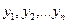(оис.3.6,в) и найдем сумму произведений заданных сил на ординаты линии влияния, взятые под точками их приложения. Согласно физическому смыслу ординат линии влияния, эта сумма будет равна величине усилия, возникающего в заданной опоре или в заданном сечении стержневой системы от действия сосредоточенных сил, т.е.:

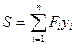(3.9)

Загрузим ту же линию влияния равномерно распределенной нагрузкой интенсивностью 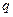(рис3.7).

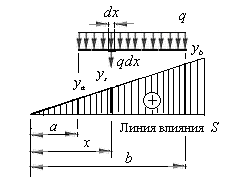
Рис.3.7

Заменим распределенную нагрузку системой бесконечно большого числа элементарных сосредоточенных сил, равных 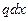. Одна из них показана на рис.3.7. Примем за начало координат нулевую точку линии влияния и обозначим ординаты линии влияния на границах участка распределенной нагрузки и под силой 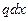через 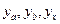соответственно.

Тогда элементарна величина усилия, возникающего от действия одной элементарной сосредоточенной силы 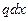, будет равна:

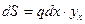(3.10)

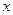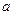Интегрируя выражение (3.10) в пределах изменения переменной от до 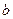, получим:

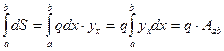(3,11)

Таким образом, величина усилия, вызванного действием равномерно распределенной нагрузки, равна произведению интенсивности этой нагрузки на площадь линии влияния в пределах участка загружения.

Примечание: При использовании формул (3.9) и (3.11) ординаты и площади линии влияния принимать с их знаками.

Загрузим линию влияния усилия 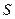сосредоточенным моментом, направленным по ходу часовой стрелки (рис.3.8). Направленный таким образом момент принимается со знаком плюс. При действии момента против хода часовой стрелки, его следует принимать со знаком минус.

Заменим действие сосредоточенного момента парой сил, имеющей произвольное плечо 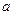. Модули сил определяются отношением величины момента к выбранной длине плеча пары сил, т.е. .

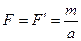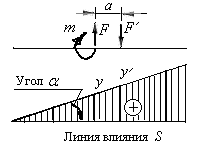
Рис.3.8

Обозначим ординаты линии влияния под силам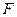и и 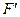буквам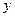и и 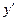соответственно. Определим величину усилия от действия дух сил по формуле (3.9). При этом силу 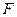принимаем со знаком минус, как направленную вверх.

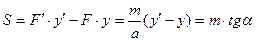(3.12)

Таким образом, величина усилия, воззванного действием сосредоточенного момента равна произведению момента на тангенс острого угла наклона линии влияния к горизонтальной прямой. Указанное произведение принимается со знаком плюс, если направление действия момента совпадает с направлением поворота линии влияния на острый угол 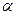до совмещения с горизонтальной прямой. Если же указанные направления не совпадают, то произведение момента на тангенс угла наклона принимается со знаком минус.

При загружении стержневой системы всеми нагрузками одновременно, усилия по линиям влияния определяют алгебраическим суммированием результатов действия каждой нагрузки в отдельности, т.е. используя принцип независимого действия сил.

Вычислим вертикальную реакцию опоры В и внутренние усилия в сечениях 1 и 2 трехпролетной балки по линиям влияния, построенным в примере 3.3. Балка загружена двумя сосредоточенными силами, моментом и распределенной нагрузкой (рис3.5,а).

Определяем ординаты линий влияния под внешними силами и на границах распределенной нагрузки. Ординаты следует вычислять с точностью до третьей значащей цифры после запятой. На рис.5.3 указаны значения ординат, выделенных жирными линиями.

Вычисляем реакцию опоры , используя формулы (3.9), (3.11) и (3.12) . Для удобства сделаем копию рис.5.3, сохранив на нем нагрузки и линию влияния .

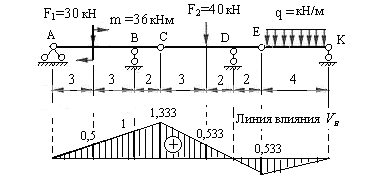
Рис.3.9

Тогда получим:

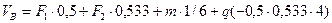
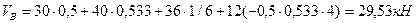
Вычисляем внутренние усилия в опорном сечении 1 трехпролетной балки. По рис.3.10 устанавливаем, что изгибающий момент и поперечная сила в заданном сечении возникают от силы 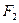и распределенной нагрузки 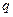. Используя формулы (3.9), (3.11), находим:

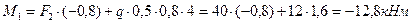
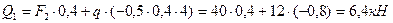
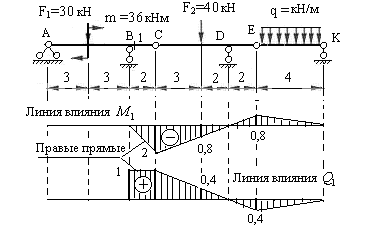
Рис.3.10

Вычисляем внутренние усилия в сечении 2 той же балки. Линии влияния этих усилий представлены на рис.3.11.

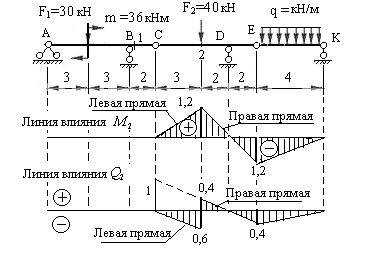
Рис.3.11

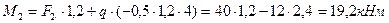
Так как линия влияния поперечной силы в сечении 2 имеет скачок под силой 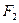, то необходимо вычислять два значения этой силы: левое и правое. При вычислении левого значения поперечной силы необходимо силу 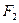умножать на правую ординату линии влияния, т.е. на 0,4, а при вычислении правого значения поперечной силы внешнюю сиу 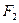следует умножать на левую ординату линии влияния, т.е. на 0,6.

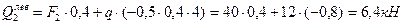
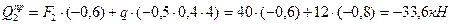
Сравним величины реакции опоры и внутренних усилий в заданных сечениях 1 и 2 трехпролетной балки.

Наименование усилий	Величины, вычисленные	% расхождения
Аналитически (по эпюрам)	По линиям влияния
	29,53	29,53
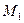
	-12,8	-12,8
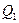
	6,4	6,4
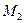
	19,2	19,2
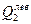
	6,4	6,4
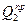
	-33,6	-33,6