Глава 3. Линии влияния и вычисление усилий от неподвижных нагрузок с использованием линий влияния.
Статический метод построения линий
Влияния.
Линией влияния некоторого силового фактора (реакции опоры или усилия в одном заданном сечении стержневой системы) называют график изменения этого фактора при движении единичного груза F=1 вдоль линии движения, связанной со стержневой системой.
При этом подвижный груз F=1перемещается медленно, не вызывая появления сил инерции системы, т.е. его движение не сопровождается динамическим эффектом действия.
При построении линий влияния следует различать непосредственный способ и узловой способ передачи подвижного груза F=1на систему. В первом случае линия движения груза совмещается со стержнями рассматриваемой системы в каждой токе, а во втором случае линия движения груза опирается на стержни в отдельных точках (узлах) и передает действие груза на систему через эти узлы. На рис.3.1 показана двухопорная балка, загруженная подвижным грузом F=1 при непосредственном способе передача его действия, а на рис.3.2 показана та же балка при узловом способе передачи того же груза. Следует обратить внимание на то, что при узловом способе передачи нагрузки линия движения опирается только на два смежных узла, предавая свое действие на балку только через эти узлы.
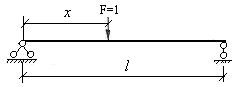
Рис.3.1
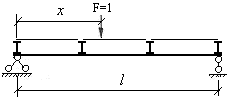
Рис.3.2
Для построения линий влияния опорных реакций и внутренних усилий в заданном сечении стержневой системы статическим способом необходимо:
1) установить груз F=1на линию движения, совмещенную с осями стержней (при непосредственной передаче действия этого груза), или опирающуюся на смежные узлы (при узловой передачи действия груза) на переменном расстоянии 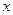 от начала координат и в этом положении принять его условно неподвижным;
от начала координат и в этом положении принять его условно неподвижным;
2) выбрать опору или сечение системы, задать силовой фактор и составить уравнение его линии влияния;
3) построить график полученного уравнения, который является линией влияния выбранного фактора.
При построении линий влияния откладывают ординаты со знаком плюс вверх от нулевой прямой, а ординаты со знаком минус - вниз от нулевой прямой, которая всегда расположена горизонтально.
Следует иметь в виду, что любая ордината линии влияния выражает величину и направление (знак ) силового фактора от действия груза F=1, расположенного над этой ординатой. В этом состоит физический смысл линий влияния.
Рассмотрим несколько примеров построения линий влияния.
Пример 3.1. Построить линии влияния опорных реакций и внутренних усилий в пролетном сечении двухкосольной балки (рис.3.3,а).
Совместим линию движения груза F=1 с осью балки и устанавливаем его на переменном расстоянии 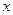 от левой опоры. В этом положении принимаем груз условно неподвижным. Тогда возникнут вертикальные реакции опор
от левой опоры. В этом положении принимаем груз условно неподвижным. Тогда возникнут вертикальные реакции опор 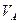 и
и  .
.
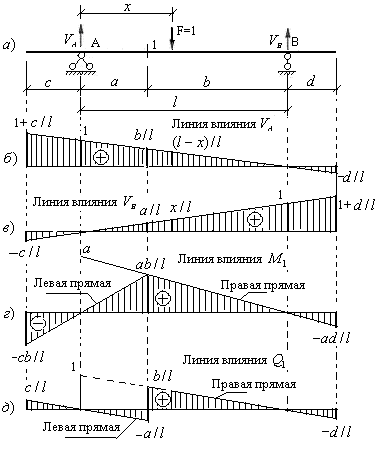
Рис.3.3
Их величины определяем из условий равновесия балки:
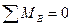 и
и 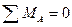
Составляем уравнения равновесия:
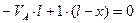

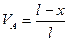 (3.1)
(3.1)
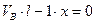

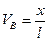 (3,2)
(3,2)
Полученные уравнения являются уравнениями линий влияния вертикальных реакций опор рассматриваемой балки. Они справедливы в интервале изменения переменной 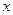 от –с до
от –с до 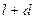 , т.е в интервале (
, т.е в интервале (  ).
).
Уравнения (3.1) и (3.2) линейные относительно переменной 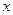 , следовательно, линии влияния реакций опор ограничены непрерывными прямыми по всей длине балки. Для их построения вычисляем по две ординаты (под опорами, либо на концах балки).
, следовательно, линии влияния реакций опор ограничены непрерывными прямыми по всей длине балки. Для их построения вычисляем по две ординаты (под опорами, либо на концах балки).
При 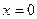 , имеем:
, имеем: 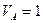 , а
, а 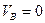
При 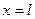 , имеем
, имеем  , а
, а 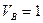
Откладываем под опорой А ординату равную 1 вверх от нулевой прямой и нулевую ординату под опорой В и соединяем прямой, продлив её до концов балки. Получаем линию влияния реакции опоры VA. Ординаты на концах балки можно вычислить из подобия треугольников, либо по уравнению (3.1) при 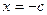 и
и 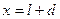 . Аналогично строим линию влияния реакции опоры В. На рис.3.3,б и 3.3,в показаны линии влияния вертикальных реакций опор двухконсольной балки.
. Аналогично строим линию влияния реакции опоры В. На рис.3.3,б и 3.3,в показаны линии влияния вертикальных реакций опор двухконсольной балки.
Перейдем к построению линий влияния внутренних усилий в пролетном сечении 1 заданной балки. Так как сечение 1 рассекает балку и линию движения груза F=1,то необходимо рассматривать два участка перемещения груза: слева и справа от сечения и составлять уравнения левых и правых прямых линий влияния изгибающего момента и поперечной силы.
Рассмотрим сначала движение груза F=1 справа от сечения 1 и составим уравнения правых прямых линий влияния внутренних усилий, использую условия равновесия левой части балки, которая загружена только реакцией 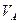 (см.рис.3.3,а).
(см.рис.3.3,а).
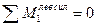

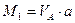 (3.3)
(3.3)
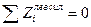

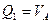 (3.4)
(3.4)
Из уравнения (3.3) следует, что правая прямая линии влияния изгибающего момента совпадает с линией влияния реакции опоры А, если её ординаты умножить на расстояние от сечения до этой опоры, т.е. на величину 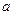 . Линия влияния
. Линия влияния 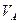 под сечением 1 имеет ординату равную
под сечением 1 имеет ординату равную 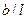 . Умножим её на
. Умножим её на 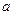 получим ординату правой прямой линии влияния изгибающего момента под заданным сечением. Она равна
получим ординату правой прямой линии влияния изгибающего момента под заданным сечением. Она равна 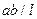 . Правая прямая проходит через нулевую точку под опорой В.
. Правая прямая проходит через нулевую точку под опорой В.
Из уравнения (3.4) следует, что правая прямая линии влияния поперечной силы совпадает с линией влияния реакции опоры А, т.е под сечением она имеет ординату равную 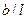 . Легко заметить, что продолжение правой прямой линии влияния изгибающего момента влево отсекает на левой опорной вертикали отрезок численно равный расстоянию от сечения до этой вертикали. Аналогично, продолжение правой прямой линии влияния поперечной силы влево, отсекает на левой опорной вертикали отрезок численно равный 1. (см.рис.3.3,г и д).
. Легко заметить, что продолжение правой прямой линии влияния изгибающего момента влево отсекает на левой опорной вертикали отрезок численно равный расстоянию от сечения до этой вертикали. Аналогично, продолжение правой прямой линии влияния поперечной силы влево, отсекает на левой опорной вертикали отрезок численно равный 1. (см.рис.3.3,г и д).
Рассмотрим далее движение груза F=1 слева от сечения 1 и составим уравнения левых прямых линий влияния внутренних усилий, использую условия равновесия правой части балки, которая загружена только реакцией  .
.
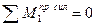

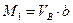 (3.5)
(3.5)
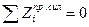

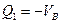 (3.6)
(3.6)
Умножив ординаты линии влияния  , взятые на левом конце балки и под сечением 1, соответственно на коэффициенты при
, взятые на левом конце балки и под сечением 1, соответственно на коэффициенты при  в уравнениях (3.5) и (3.6) получаем ординаты левых прямых линий изгибающего момента и поперечной силы (см.рис.3.3,г и д).
в уравнениях (3.5) и (3.6) получаем ординаты левых прямых линий изгибающего момента и поперечной силы (см.рис.3.3,г и д).
Анализируя линии влияния внутренних усилий в пролетном сечении двухкосольной балки легко выявить следующие их свойства:
1) Линии влияния изгибающего момента и поперечной силы ограничены двумя прямыми: левой - слева от сечения и правой - справа от сечения;
2) Левые прямые имеют нулевые ординаты под левой опорой балки, а правые прямые имеют нулевые ординаты под правой опорой балки;
3) Левая и правая прямые линии влияния изгибающего момента пересекаются под сечением, образуя максимальную ординату равную отношению произведения отрезков, на которые сечение делит пролет, к его длине.
4) Левая и правая прямые линии влияния поперечной силы параллельны между собой.
Эти свойства позволяют построить линии влияния внутренних усилий в любом пролетном сечении балки, опирающейся на две шарнирные опоры.
Пример 3.2. Построить линии влияния внутренних усилий в опорных сечениях двухкосольной балки (рис.3.4,а).
Особенность опорных сечений балки состоит в том, что в них действуют сосредоточенные силы, т.е. реакции опор, которые вызывают разрыв поперечных сил в этих сечениях. Поэтому при построении линий влияния поперечных сил необходимо опорные сечения относить к пролету балки и к её консоли.
Рассмотрим опорное сечение А балки (3.4,а). Сдвинем его чуть влево, получим сечение 2, отнесенное к консоли, При смещении опорного сечения чуть вправо, получим сечение 3, отнесенное к пролету балки.
Построим линии влияния внутренних усилий в сечении 2.
При движении груза F=1 слева от сечения 2 составляем уравнения левых прямых из условий равновесия левой отсеченной части, на которую действует только этот груз. Составляем уравнения левых прямых из условий:
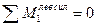

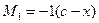 (3.7)
(3.7)
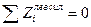

 (3.8)
(3.8)
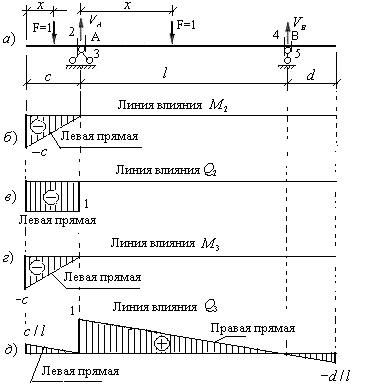
Рис.3.4
Из уравнения (3.7) следует, что левая прямая линии влияния изгибающего момента имеет ординату равную 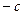 на конце консоли и нулевую ординату под опорой А.
на конце консоли и нулевую ординату под опорой А.
Из уравнения (3.8) следует, что левая прямая линии влияния поперечной силы параллельна нулевой прямой и отстоит от неё на величину равную -1.
При движении груза F=1 справа от сечения 2 усилия в этом сечении не возникают, что вытекает из условий равновесия левой незагруженной части балки. Следовательно, правые прямые сливаются с нулевыми прямыми.
На рис.3.4,б и в построены линии влияния 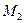 и
и 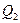 .
.
Для построения линий влияния внутренних усилий в сечении 3, исследуем изменение линий влияния внутренних усилий в пролетном сечении 1, если это сечение постепенно смещать к опоре А, т. е. к сечению 3.
Рассмотрим линию влияния 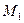 (рис.3.3,г). При сближении сечения 1 с сечением 3 правая прямая удлиняется, а максимальная ордината под сечением уменьшается и обращается в нуль при совмещении указанных сечений. Ордината левой прямой на конце консоли будет равна
(рис.3.3,г). При сближении сечения 1 с сечением 3 правая прямая удлиняется, а максимальная ордината под сечением уменьшается и обращается в нуль при совмещении указанных сечений. Ордината левой прямой на конце консоли будет равна 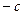 , а под опорой А равна нулю.
, а под опорой А равна нулю.
Рассмотрим линию влияния 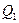 . При сближении сечений 1 и 3 левая прямая укорачивается, а правая прямая удлиняется, оставаясь параллельными между собой. Тогда в пределе под опорой А правая прямая будет иметь ординату равную 1, а левая прямая – равную нулю. На рис.3.4,г и д построены линии влияния
. При сближении сечений 1 и 3 левая прямая укорачивается, а правая прямая удлиняется, оставаясь параллельными между собой. Тогда в пределе под опорой А правая прямая будет иметь ординату равную 1, а левая прямая – равную нулю. На рис.3.4,г и д построены линии влияния 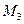 и
и 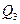 .
.
Предлагаем изучающим курс построить линии влияния внутренних усилий в сечениях 4 и 5 балки, представленной на рис 3.4,а.
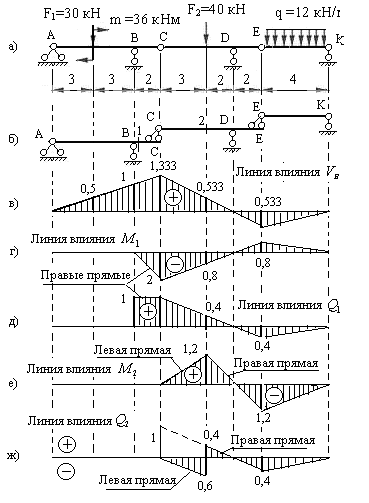
Рис.3.5
Пример 3.3. Построить линии влияния реакции опоры В и усилий в сечениях 1 и 2 заданной трехпролетной балки (рис.3.5,а).
Заданная балка состоит из трех дисков: главного диска AC, передаточного диска CE и подвесного диска EK. Поэтажная схема балки представлена на рис.3.5,б.
Опора В и сечение 1 принадлежат главному диску, а сечение 2 – передаточному диску. Построение линий влияний для многопролетных балок осуществляется статическим методом с использованием свойств, установленных в примерах 3.1 и 3.2. При этом сначала необходимо построить линии влияния в пределах диска, которому принадлежит заданная опора или сечение, а затем достроить линии влияния в пределах вышележащих дисков поэтажной схемы, используя следующие правила:
1) В пределах каждого вышележащего диска линия влияния любого фактора непрерывна, прямолинейна и проходит через нулевую точку под наземной опорой;
2) На стыке двух дисков (под шарнирами) линия влияния любого фактора имеет общие ординаты для двух объединяемых дисков.
Следует иметь в виду, что при движении груза F=1 вдоль нижележащих дисков, усилия в опорах и сечениях вышележащих дисков не возникают.
Построим линию влияния вертикальной реакции  (рис.3.5,в). Для этого отложим под опорой В вверх от нулевой прямой ординату равную 1 и проведем из её вершины прямую через нулевую точку, взятую под опорой А. Эта прямая ограничивает линию влияния в пределах главного диска АС. Величину ординаты под шарниром С вычисляем из подобия треугольников. Она равна 1,333.
(рис.3.5,в). Для этого отложим под опорой В вверх от нулевой прямой ординату равную 1 и проведем из её вершины прямую через нулевую точку, взятую под опорой А. Эта прямая ограничивает линию влияния в пределах главного диска АС. Величину ординаты под шарниром С вычисляем из подобия треугольников. Она равна 1,333.
Используя приведенные выше правила, достраиваем линию влияния  в пределах передаточного и подвесного дисков. Из вершины ординаты под шарниром С проводим прямую через нулевую точку под наземной опорой D до вертикали, проходящей через шарнир E. Ордината под шарниром E равна 0,533 (из подобия треугольников). Затем соединяем вершину полученной ординаты с нулевой точкой под наземной опорой К.
в пределах передаточного и подвесного дисков. Из вершины ординаты под шарниром С проводим прямую через нулевую точку под наземной опорой D до вертикали, проходящей через шарнир E. Ордината под шарниром E равна 0,533 (из подобия треугольников). Затем соединяем вершину полученной ординаты с нулевой точкой под наземной опорой К.
Построим линии влияния изгибающего момента и поперечной силы в сечении 1(рис.3,5,г и д). Это сечение является опорным сечением главного диска, отнесенным к консоли. Если груз F=1 будет перемещаться слева от сечения, то усилия в нем будут равны нулю. Следовательно, левые прямые линий влияния будут совпадать с нулевыми прямыми.
При движении груза F=1 вдоль консоли ВС изгибающий момент в сечении 1 меняется по линейному закону от нуля до -2, а поперечная сила сохраняет постоянное значение равное 1. По этим ординатам строим правые прямые, а затем достраиваем линии влияния в пределах передаточного и подвесного дисков и вычисляем их ординаты под шарниром E.
Построим линии влияния усилий в сечении 2. Это сечение принадлежит передаточному диску CE и является пролетным. Используя установленные ранее свойства, строим линии влияния в пределах диска CE, затем достраиваем их в пределах подвесного диска EK (рис.3.5,е и ж).
Дата добавления: 2019-04-03; просмотров: 4146;
