Глава 4. Трехшарнирные стержневые системы (арки и рамы).
Элементы трехшарнирных арок, очертание их оси и характеристики оси в сечениях арки.
Трехшарнирной аркой называют стержневую систему, состоящую из двух криволинейных дисков, объединенных между собой ключевым шарниром, и закрепленных на концах шарнирно неподвижными опорами.
На рис.4.1 показана трехшарнирная арка. Её элементами являются:
- криволинейные диски АС и ВС, которые называют полуарками;
- ключевой шарнир С и опорные (пятовые) шарниры А и В;
- опорная прямая АВ, которая проходит через центры опорных шарниров;
- пролет арки  и горизонтальные проекции полуарок
и горизонтальные проекции полуарок 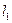 и
и 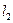 , называемые полупролетами арки;
, называемые полупролетами арки;
стрела подъема арки 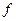 , равная расстоянию от ключевого шарнира до опорной прямой.
, равная расстоянию от ключевого шарнира до опорной прямой.
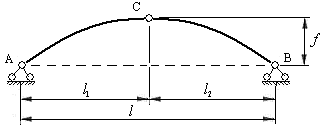
Рис.4.1
Опорные шарниры арки, как правило, располагаются в одном уровне, т.е. опорная прямая является горизонтальной прямой. С этой прямой совмещается горизонтальная ось системы координат. Начало системы координат принимается в центре левого опорного шарнира.
Очертание оси арки может быть задано уравнением квадратичной параболы или уравнением окружности. В первом случае арку называют параболической, а во втором – циркульной.
Рассмотрим трехшарнирную арку, отнесенную к системе осей 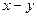 (рис.4.2).
(рис.4.2).
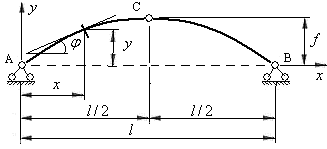
Рис.4.2
Любое сечение оси арки, взятое на расстоянии 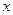 от начала координат будет иметь ординату
от начала координат будет иметь ординату 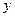 , определяемую из уравнения, принятого для очертания оси арки.
, определяемую из уравнения, принятого для очертания оси арки.
При параболическом очертании арки ордината 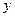 вычисляется из уравнения:
вычисляется из уравнения:
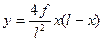 (4.1)
(4.1)
При циркульном очертании арки ордината 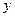 вычисляется из уравнения:
вычисляется из уравнения:
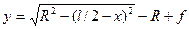 , (4.2)
, (4.2)
где 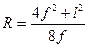 (4.3)
(4.3)
Проведем касательную к оси арки в заданном сечении и обозначим через 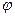 угол её наклона к горизонтальной оси
угол её наклона к горизонтальной оси 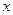 . Тогда при параболическом очертании оси арки тангенс этого угла будет определяться по формуле:
. Тогда при параболическом очертании оси арки тангенс этого угла будет определяться по формуле:
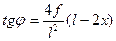 (4.4)
(4.4)
Синус и косинус того же угла находят по известным формулам тригонометрии:
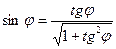 ,
, 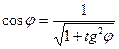 (4.5)
(4.5)
При очертании оси арки по окружности тригонометрические функции угла 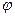 вычисляются по формулам:
вычисляются по формулам:
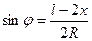 ,
, 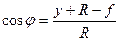 (4.6)
(4.6)
Опоры трехшарнирных арок могут располагаться в разных уровнях (рис.4.3).
Для таких арок ось 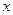 совмещается с опорной прямой АВ , а ось
совмещается с опорной прямой АВ , а ось 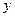 направляется перпендикулярно к оси
направляется перпендикулярно к оси 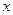 . Характеристики сечений оси арки определяются по приведенным выше формулам, при замене в них длины пролета арки длиной опорной прямой, т.е величиной
. Характеристики сечений оси арки определяются по приведенным выше формулам, при замене в них длины пролета арки длиной опорной прямой, т.е величиной 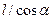 .
.
Расчет таких арок сложнее, чем арок с опорами в одном уровне и в данном пособии не приводится.
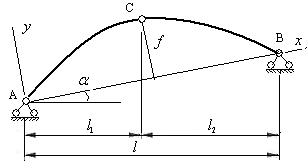
Рис.4.3
Дата добавления: 2019-04-03; просмотров: 1439;
