Итак, поперечная сила в произвольном сечении арки равна разности произведений балочной поперечной силы на косинус угла наклона касательной и распора арки на синус того же угла.
Поперечная сила в сечении принимается со знаком плюс, если она стремится повернуть любую отсеченную часть арки по часовой стрелке и со знаком минус, если она стремится повернуть любую часть арки против часовой стрелки.
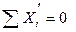

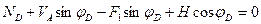
Откуда 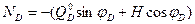 (4.20)
(4.20)
Итак, продольная сила в произвольном сечении арки равна взятой со знаком минус сумме произведений балочной поперечной силы на синус угла наклона касательной и распора арки на косинус того же угла.
Продольная сила принимается со знаком плюс, если она вызывает растяжение арки в данном сечении, т.е. направлена от сечения. Продольная сила принимается со знаком минус, если она вызывает сжатие арки в данной сечении, т.е направлена к сечению.
Внутренние усилия в заданном сечении трехшарнирной арки вычисляются по формулам (4.18 – 4.20) в следующем порядке:
- Определяются вертикальные реакции опор и распор трехшарнирной арки, а также вертикальные реакции однопролетной балки, имеющей тот же пролет и загруженной теми же нагрузками, что и арка;
- Вычисляются усилия в сечении балки, расположенном на одной вертикали с заданным сечением арки (балочные усилия 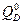 и
и 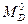 );
);
- Вычисляются геометрические параметры оси арки в заданном сечении, т.е. величины:
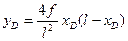 ;
; 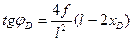 ;
;
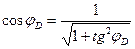 ;
; 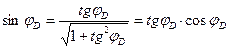 ;
;
- Вычисляют усилия в заданном сечении арки по формулам (4.18 – 4.20).
Пример 4.1. Для заданной арки (рис.4.11,а) требуется вычислить усилия в сечениях 1 и 2, если арка загружена силами: 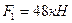 ,
, 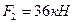 ,
, 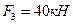 ,
, 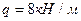 . Размеры в метрах показаны на рис.4.11,а. На рис.4.11,б показана двухопорная балка, имеющая тот же пролет и загруженная теми же нагрузками, что и арка.
. Размеры в метрах показаны на рис.4.11,а. На рис.4.11,б показана двухопорная балка, имеющая тот же пролет и загруженная теми же нагрузками, что и арка.
Решение:
- Вычисляем вертикальные реакции опор трехшарнирной арки по формулам (4.12) и (4.13):
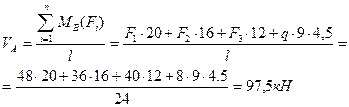
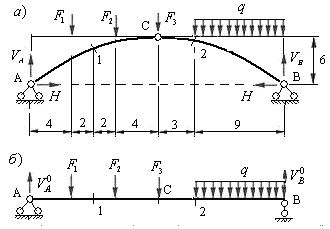
Рис.4.11
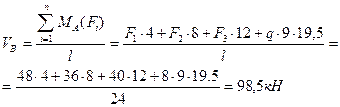
Проверка: 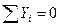

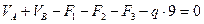
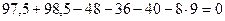

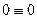
Вертикальные реакции опор балки, приведенной на рис.4.11,б, равны вертикальным реакциям соответствующих опор арки.
Вычисляем распор арки по формуле (4.15)
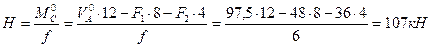
Для проверки вычисленного распора составляем уравнение равновесия правой полуарки относительно левой, т.е.:
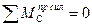

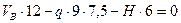

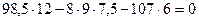

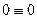
- Вычисляем балочные усилия в сечениях 1 и 2:
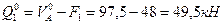 ,
,
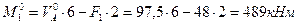 .
.
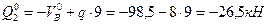
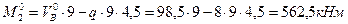
- Вычисляем геометрические параметры оси арки в сечениях 1 и 2:
Сечение 1:
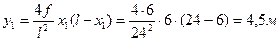
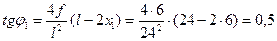 ;
; 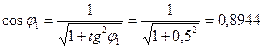
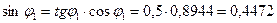
Сечение 2:
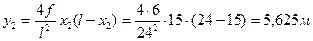 ;
; 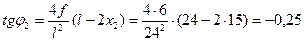
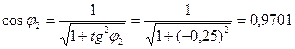 ;
; 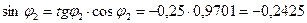
- Вычисляем усилия в заданных сечениях 1 и 2 арки, используя формулы (4.18 – 4.20):
Сечение 1:
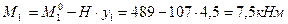
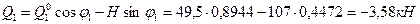
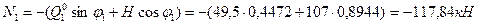
Сечение 2
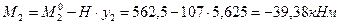
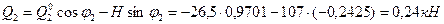
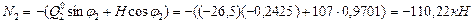
Дата добавления: 2019-04-03; просмотров: 848;
