В соответствии с основным принципом динамики равнодействующая всех сил равна массе, умноженной на ускорение.
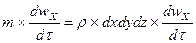
Т.е. равновесие сил (после сокращенных)
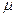 Ñ2wx -
Ñ2wx - 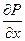 =
= 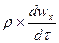 Уравнение Навье-Стокса для одномерного давления
Уравнение Навье-Стокса для одномерного давления
При трехмерном движении:
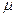 Ñ2wy -
Ñ2wy - 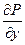 =
= 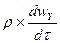
- 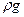 +
+ 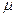 Ñ2wz -
Ñ2wz - 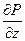 =
= 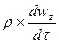
При движении идеальной жидкости, движущая без трения, получим:
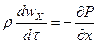
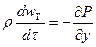 Диф. уравнения движения идеальной жидкости Эйлера.
Диф. уравнения движения идеальной жидкости Эйлера.
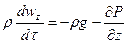
Полное описание движения вязкой жидкости возможно только при совместном решении уравнений Н-Стокса и уравнения неразрывности потока с помощью теории подобия.
III. Уравнение Бернулли –отражает закон сохранения энергии, выводится преобразованием уравнения Эйлера. Запишем выражение для проекции сил на ось z:
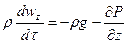 (1)
(1)
Заменим 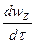 на
на 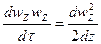 где
где 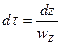 т.к
т.к 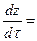 wz
wz
В Ур-е (1) заменим частные диференциальные на полный и умножим на 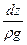
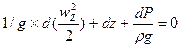
липолный и умножим на ения – тор Лапласа сумма 2ых производных.
опорциональная поверхностиили 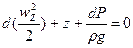 откуда
откуда 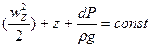 – Ур-е Бернулли.
– Ур-е Бернулли.
Для любых двух сечений потока
Рисунок! z1 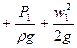 = z2
= z2 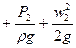 -величина над. полным гидродинамическим напором.
-величина над. полным гидродинамическим напором.
Закон Бернулли:гидродинамический напор для 2ух сечений установившегося потока идеальной жидкости есть величина постоянная.
Z=h2 – Нивелирная или геометрическая высота, характеризует потенциальную энергию P/pg = Hст – Статическийили скоростной напор, характеризует потенциальную энергию давления в данной точке.
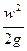 – Динамическийили скоростной напор, характеризует кинетическую энергию.
– Динамическийили скоростной напор, характеризует кинетическую энергию.
Дата добавления: 2017-08-01; просмотров: 698;
