Подобные преобразования уравнения
Навье-Стокса
Как уже говорилось, уравнение Н-Стокса не решается аналитически применительно к задачам турбулентных течений, поэтому не удается теоретически получить расчет вне зависимости для определения потерь энергии (напора). Поэтому приведем их подобные преобразования.
Запишем уравнение Н-Стокса для оси z
- 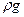 +
+ 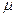 Ñ2wz -
Ñ2wz - 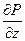 =
= 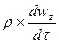 (1)
(1)
Распишем оператор Лапласа, силу инерции, разделим (1) на ρ и запишем уравнение Н-стокса для изменения только вдоль оси х, где V=μ/ρ
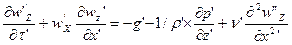 (2)
(2)
Это уравнение для натуры. Запишем для модели
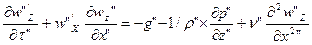 По достаточным условием подобие ???? уравнения для натуры и модели д.б. равны, т.е. (2)=(3)
По достаточным условием подобие ???? уравнения для натуры и модели д.б. равны, т.е. (2)=(3)
В соответствии с необходимыми условиями подобия все константы для модели и натуры д.б. одинаковы и можем записать
K τ= τ’/ τ” Кg=g’/g” Kl=l’/l” Kp=p’/p” (4)
Мы должны выразить уравнение натуры (2) через модель, подставляя следующее выражение (5)
τ’=K*τ” g’=Kg*g” l’=Kl*l” p’=Kp*p”(5)
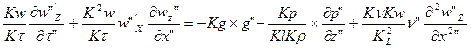
По достаточным условиям (6) д.б = (3), а это возможно, если коэффициенты в уравнении (6) равны
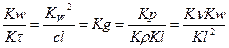
Распишем 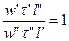 или
или 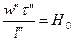
1) Но – критерий гомохронности-временное подобие, характер неустановившейся процесс в гидродинамике
Рассмотрим вторую пару
2)Kw2 / Kl=Kg и получим w2/lg=Fr – критерий Фруда
Характеризует соотношение силы инерции и силы тяжести в подобных системах.
Все соотносим с силой инерции !!!
Kw2 / Kl=Kp/K 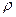 Kl : (Kw2)
Kl : (Kw2)
3)DP/ 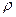 w2=Eu критерий Эйлера– характеризует соотношение м/у силой давления и силой инерции в подобных системах
w2=Eu критерий Эйлера– характеризует соотношение м/у силой давления и силой инерции в подобных системах
Kw2 / Kl= 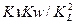
4) 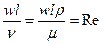 критерий Рейнольдса –характеризует отношение сил инерции к силе трения.
критерий Рейнольдса –характеризует отношение сил инерции к силе трения.
Кроме 4ех основных критериев существуют вспомогательные (путем ХМ:)
У Fr 3 аналога
Галилея 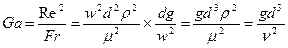
Архимеда 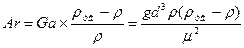
Грисгофа Gr=Ga * 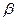 *Dt– для описания тепловых процессов.
*Dt– для описания тепловых процессов.
Теоремы подобия
I Теорема
Критерии описывающие процесс для натуры и модели должны быть численно равны.
Теорема ставит вопрос: как построить модель и какие величины измерить при проведении опыта.
Ответ: чтобы критерии для модели и натуры были одинаковы измерить те величины, которые входят в критерии.
Дата добавления: 2017-08-01; просмотров: 550;
