II. Дифференциальное уравнение движения вязкой несжимаемой жидкости (уравнение Навье-Стокса)

При движении реальной жидкости в потоке жидкости помимо сил давления и тяжести действуют так же силы трения. Выделим в потоке элементарный объем dv=dx dy dz

Сделаем допущения: 1) движение одномерное, т.е. вдоль оси х.

РИСУНОК!!

2) верхний слой более медленный.

3) проекция составляющей скорости Wx зависит только от расстояния Z до горизонтальной плоскости отчета.

Рассмотрим силы, действующие на элемент. Объем:

(G – сила тяжести вдоль оси z)

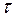– Касательное напряжение на нижний грани.

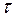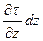( + )– то же для верхний грани

Тогда проекция равнодействующей сил трения на ось х:

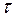dx dy - ( 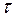+ 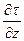dz)dxdy=- 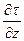dxdydz а так как касательное напряжение =

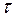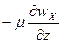
То 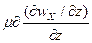dxdydz= 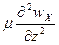dxdydz

В случае трехмерного потока составляющая скорости их будет изменяться не только в направлении z, но и в направлении всех трех осей координат

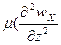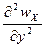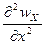+ + )dxdydz выражение называется оператор Лапласа сумма 2ых производных ѲWx

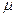Ѳw_x dxdydz – сила трения вдоль оси х.

Кроме того что по оси х действует составляющая cилы гидростатического давления –

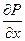- dxdydz