Основные законы гидродинамики.
I. Уравнение неразрывности потока. –отражает мат. баланс системы или закон сохранения массы.
РИСУНОК Выделим внутри потока элементарный объем жидкости
dv=dx dy dz
Так как в ХТ процессах скорость и плотность величины переменные в пространстве и времени, то u= f(X, Y, Z, τ) и p= f(X, Y, Z, τ)
Общий массовый расход G=p*u*S
Тогда в направлении оси Х за промежуток времени dτ в элемент. Объем войдет масса жидкости Gx =r*Wx*dy*dz*d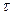
На противоположной грани на расстоянии dx за счет изменения выйдет кол-во вещества
Gx+dx=(r*Wx+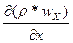 
)dx dy dz d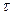
Приращение массы жидкости в объеме вдоль оси х:
dGx =Gx- Gx+dx =-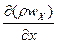 
dx dy dz d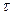
По аналогии вдоль осей y и z
dGy=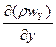 
dx dy dz d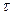
dGz=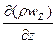 
dx dy dz d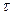
Суммарное приращение массы составит
dG=-( 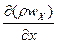+ + 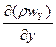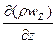) dx dy dz d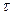
Т.к изменение массы в замкнутом объеме возможно только вследствие изменения плоскости, то dG=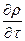 
dx dy dz d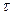
Приравняем уравнение (1) и (2) и сократим на uvdT и получим
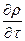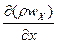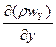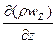+ + + =0
Это дифферинциальное уравнение неразрывности потока для неустановившегося движения сжимаемой жидкости. В установившемся потоке плотность не изменяется во времени, т.е. 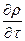=0
И уравнение принимает вид:
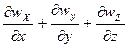=0
Дифференциальное уравнение неразрывности потока сжимаемой жидкости при установившемся режиме движения вдоль оси х.и с учетом поперечного сечения потока имеет вид:
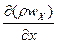=0
Или в иннженерной форме 
ws=const
Т.е. для трех различных сечений имеет S1 1 w 1= S2 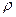2 w 2= S3 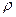3 w 3или G1=G2=G3
Это выражение называется уравнение постоянства расхода при установившемся движении жидкости, полностью заполняющий трубопровод, через каждое его поперечное сечение проходит в единицу времени одно и тоже количество жидкости.
Для капельной жидкости S1w 1= S2w 2= S3w 3 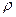=const
откуда следует, что скорости капельной жидкости в различных поперечных сечениях трубопровода обратно пропорционально площади этих сечений.
Дата добавления: 2017-08-01; просмотров: 578;