II. Дифференциальное уравнение движения вязкой несжимаемой жидкости (уравнение Навье-Стокса)
При движении реальной жидкости в потоке жидкости помимо сил давления и тяжести действуют так же силы трения.
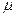Ñ2wx - 
= 
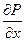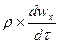Уравнение Навье-Стокса для одномерного давления
При трехмерном движении:
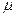Ñ2wy - 
= 
- 
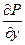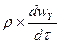
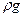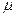+ Ñ2wz - 
= 
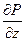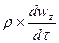
При движении идеальной жидкости, движущейся без трения, получим:
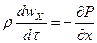
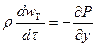Диф. уравнения движения идеальной жидкости Эйлера.
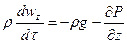
III. Уравнение Бернулли –отражает закон сохранения энергии, выводится преобразованием уравнения Эйлера.
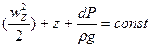– Уравнение Бернулли для идеальной жидкости
Для любых двух сечений потока
z1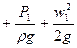 
= z2 
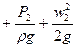-величина над. полным гидродинамическим напором.
Закон Бернулли:гидродинамический напор для 2-х сечений установившегося потока идеальной жидкости есть величина постоянная.
Z=h2 – Нивелирная или геометрическая высота, характеризует удельную потенциальную энергию
P/pg = Hст – Статическийили пьезометрический напор, характеризует потенциальную энергию давления в данной точке.
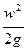– Динамическийили скоростной напор, характеризует кинетическую энергию.
Дата добавления: 2017-08-01; просмотров: 730;