Если сосуд под вакуумом, то прибор показывает разрежение Рвак.
и Рабс.=Ратм.-Рвак.
Гидростатика
Как уже говорилось, гидростатика изучает законы равновесие жидкостей, находящихся в состоянии относительного покоя. Т.е. в движущейся жидкости ее частицы не перемещаются друг относительно друга. И силы внутреннего трения отсутствуют.
Пример: цистерна с жидкостью, покой рассматривается относительно стенок.
Основным уравнением гидростатики является дифференциальное уравнение равновесия Эйлера
В объеме жидкости, находящейся в покое, выделим элементарный объем жидкости dVc ребрами dx, dy и dz.
dv=dx*dy*dz
Сила тяжести, действующая на выделенным объем жидкости, выражается произведением его массы dm на ускорение свободного падения G = -gdm = -gρdV = -gρdxdydz
Сила гидростатического давления на любую из граней равна произведению гидростатического давления ρ на площадь этой грани.
Общее давление, действующее на нижнюю грань можно определить как:
Рнобщ = pdxdy
Гидростатическое давление, действующее на верхнюю грань можно представить как:
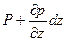где
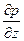– частное производное гидростатического давления вдоль оси z;
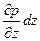-положительное приращение гидростатического давления вдоль оси z.
Общее давление на верхнюю грань
Pвобщ=( 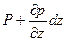)dxdy
Так как согласно основному принципу статики, сумма проекций на оси координат всех сил, действующих на элементарный объем, находящийся в равновесии, равна нулю, то можно записать
-G+ Рнобщ- Рвобщ=0
-gρdxdydz+pdxdy-( 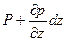)dxdy=-gρdxdydz+ pdxdy- pdxdy- 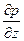dxdydz=o
Учитывая, что объем жидкости не равен 0 (dV+/-0) можно сократить на dV
И получим –gρ- 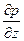=0
Проекция сил тяжести на оси x и y =0
Поэтому проекции сил на оси x и y равны
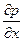=0
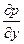=0 Дифференциальное уравнение равновесия Эйлера
–gρ- 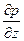=0
Из уравнений следует, что давление в покояшейся жидкости изменяется только по вертикали (вдоль оси z), оставаясь одинаковым во всех точках любой горизонтальной плоскости, т.к. изменение давлений вдоль осей x и y равны нулю.
Заменив частную производную 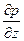на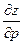 
и домножив обе части уравнения на dz и сменив знаки получим +ρgdz+dp=0
Разделив обе части на ρg получим dz + dp/ρg =0
И проинтегрировав получим
z+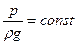 
– Это основное уравнение гидростатики
Для двух произвольных горизонтальных плоскостей уравнение используется в виде
РИСУНОК z1+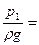 
z2+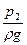 
Z – высотный напор или нивелирная высота, характеризующую потенциальную энергию положения в данной точке на выбранной плоскостью сравнения.
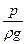– пьезометрический или статический напор – характеризует удельную энергию, т.е. энергию, приходящуюся на единицу веса жидкости или удельную потенциальную энергию давления в данной точке.
z+ 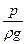– полный гидростатический напор.Основное уравнение гидростатики представляет собой частный случай закона сокращения энергии: удельная потенциальная энергия во всех точках покоящейся жидкости есть величина постоянная.
Размерность Z и 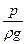в ед. длины – м
[ ]= 
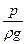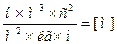
Основное уравнение гидростатики можно записать в виде
p 1+ρgz1= p 2+ρgz2 или p 2=ρg(z1- z2)
Закон Паскаля
Дата добавления: 2017-08-01; просмотров: 580;