Анализ взаимосвязанных рядов динамики

В простейших случаях для характеристики взаимосвязи двух или более рядов их приводят к общему основанию , для чего берут в качестве базисных уровни за один и тот же период и исчисляют коэффициенты опережения по темпам роста или прироста .

Коэффициенты опережения по темпам роста – это отношение темпов роста (цепных или базисных) одного ряда к соответствующим по времени темпам роста (также цепным или базисным) другого ряда . Аналогично находятся и коэффициенты опережения по темпам прироста .

Анализ взаимосвязанных рядов представляет наибольшую сложность при изучении временных последовательностей . Однако нередко совпадение общих тенденций развития может быть вызвано не взаимной связью , а прочими неучитываемыми факторами . Поэтому в сопоставляемых рядах предварительно следует избавиться от влияния существующих в них тенденций , а после этого провести анализ взаимосвязи по отклонениям от тренда . Исследование включает проверку рядов динамики (отклонений) на автокорреляцию и установление связи между признаками .

Под автокорреляцией понимается зависимость последующих уровней ряда от предыдущих . Проверка на наличие автокорреляции осуществляется по критерию Дарбина – Уотсона (формула 39) :

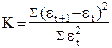, (39)

где 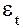-- отклонение фактического уровня ряда в точке t от теоретического (выровненного) значения .

При К = 0 имеется полная положительная автокорреляция , при К = 2 автокорреляция отсутствует , при К = 4 – полная отрицательная автокорреляция . Прежде чем оценивать взаимосвязь , автокорреляцию необходимо исключить . Это можно сделать тремя способами .

1. Исключение тренда с авторегрессией. Для каждого из взаимосвязанных рядов динамики Х и У получают уравнение тренда (формулы 40) :

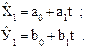(40)

Далее выполняют переход к новым рядам динамики , построенным из отклонений от трендов , рассчитанным по формулам 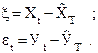41 :

(41)

Для последовательностей 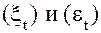выполняется проверка на автокорреляцию по критерию Дарбина – Уотсона . Если значение К близко к 2 , то данный ряд отклонений оставляют без изменений . Если же К заметно отличается от 2 , то по такому ряду находят параметры уравнения авторегрессии по формулам 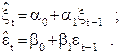42 :

(42)

Более полные уравнения авторегрессии можно получить на основе анализа автокорреляционной функции , когда определяются число параметров ( 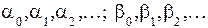) и соответствующие этим параметрам величины шагов .

Далее по формуле 43 подсчитываются новые остатки :

(t = 1, ... , Т) (43)

и , по формуле 44, коэффициент корреляции признаков :

. (44)

2.Корреляция первых разностей . От исходных рядов динамики Х и У переходят к новым , построенным по первым разностям (формулы 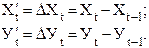45) :

(45)

По DХ и DУ определяют по формуле 46 направление и силу связи в регрессии:

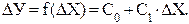(46)

3. Включение времени в уравнение связи : .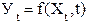

В простейших случаях уравнение выглядит следующим образом (формула 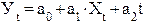47):

(47)

Из перечисленных методов исключения автокорреляции наиболее простым является второй, однако более эффективен первый.

Вопросы для самоконтроля

1. Что такое ряд и уровни ряда динамики?

2. Охарактеризуйте моментные и интервальные ряды динами­ки.

3. Какие отличия имеют моментный и интервальный ряды ди­намики?

4. Какие имеются показатели рядов динамики и для каких це­лей они применяются?

5. В чем сущность выравнивания динамических рядов спосо­бом скользящей средней?

6. Как осуществляется параболическое выравнивание динами­ческого ряда?

7. Охарактеризуйте метод конечных разностей и для каких це­лей они применяются.

8. Суть сезонности и ее значение для экономики.

9. Что представляет собой метод простой средней, который используется для анализа сезонности?

10. Дайте определение и расчет индекса сезонности.

11. Как исчисляется средняя сезонная волна из процентных отношений уровней?

12. Как осуществляется анализ сезонности?

13. В чем сущность анализа сезонности в рядах динамики после определения и исключения общей тенденции развития?