Статистические показатели динамики

Для количественной оценки динамики явлений применяются статистические показатели : абсолютные темпы роста и прироста , темпы наращивания и т. д.

В основе расчета показателей рядов динамики лежит сравнение его уровней . В зависимости от применяемого способа сопоставления показатели динамики могут вычисляться на постоянной и переменной базах сравнения .

Для расчета показателей динамики на постоянной базе каждый уровень ряда сравнивается с одним и тем же базисным уровнем . Исчисляемые при этом показатели называются базисными . Для расчета показателей динамики на переменной базе каждый последующий уровень ряда сравнивается с предыдущим . Такие показатели называются цепными .

Абсолютный прирост – важнейший статистический показатель динамики , определяется в разностном соотношении , сопоставлении двух уровней ряда динамики в единицах измерения исходной информации . Бывает цепной и базисный :

1) Базисный абсолютный прирост 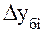определяется как разность между сравниваемым уровнем 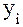и уровнем , принятым за постоянную базу сравнения 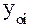(формула 1):

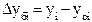(1)

2) Цепной абсолютный прирост 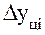– разность между сравниваемым уровнем 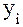и уровнем , который ему предшествует, 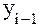(формула 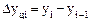2):

(2)

Абсолютный прирост может иметь и отрицательный знак , показывающий , насколько уровень изучаемого периода ниже базисного .

Между базисными и абсолютными приростами существует связь : сумма цепных абсолютных приростов 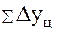равна базисному абсолютному приросту последнего ряда динамики 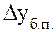(формула 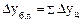3):

(3)

Ускорение – разность между абсолютным приростом за данный период и абсолютным приростом за предыдущий период равной длительности (формула 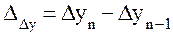4):

(4)

Показатель абсолютного ускорения применяется только в цепном варианте , но не в базисном . Отрицательная величина ускорения говорит о замедлении роста или об ускорении снижения уровней ряда .

Темп роста – распространенный статистический показатель динамики . Он характеризует отношение двух уровней ряда и может выражаться в виде коэффициента или в процентах .

1) Базисные темпы роста 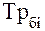исчисляются делением сравниваемого уровня 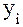на уровень , принятый за постоянную базу сравнения 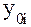, по формуле 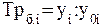5 :

(5)

2) Цепные темпы роста 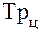исчисляются делением сравниваемого уровня 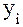на предыдущий уровень 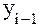(формула 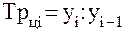6):

(6)

Если темп роста больше единицы (или 100%) , то это показывает на увеличение изучаемого уровня по сравнению с базисным . Темп роста ,равный единице (или 100%) , показывает , что уровень изучаемого периода по сравнению с базисным не изменился . Темп роста меньше единицы (или 100%) показывает на уменьшение уровня изучаемого периода по сравнению с базисным. Темп роста всегда имеет положительный знак .

Между базисными и цепными темпами роста имеется взаимосвязь : произведение последовательных цепных темпов роста равно базисному темпу роста , а частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста .

Темпы прироста характеризуют абсолютный прирост в относительных величинах . Исчисленный в процентах темп прироста показывает , на сколько процентов изменился сравниваемый уровень по отношению к уровню , принятому за базу сравнения .

1) Базисный темп прироста 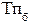вычисляется делением сравниваемого базисного абсолютного прироста 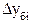на уровень , принятый за постоянную базу сравнения 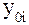(формула 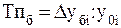7):

(7)

2) Цепной темп прироста 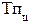-- это отношение сравниваемого цепного абсолютного прироста 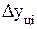к предыдущему уровню 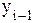(формула 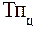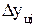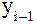8):

= : (8)

Между показателями темпа роста и темпа прироста существует взаимосвязь , выраженная формулами 9 и 10:

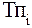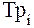(%) = (%) - 100 (9)

(при выражении темпа роста в процентах).

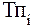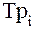= - 1 (10)

(при выражении темпа роста в коэффициентах).

Формулы (7) и (8) используют для нахождения темпов прироста по темпам роста .

Важным статистическим показателем динамики социально – экономических процессов является темп наращивания , который в условиях интенсификации экономики измеряет наращивание во времени экономического потенциала .

Вычисляются темпы наращивания Тн делением цепных абсолютных приростов 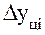на уровень , принятый за постоянную базу сравнения , 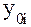по формуле 11:

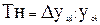(11)