Средние показатели в рядах динамики
Для получения обобщающих показателей динамики социально -- экономических явлений определяются средние величины : средний уровень , средний абсолютный прирост , средний темп роста и прироста и пр.
Средний уровень ряда динамики характеризует типическую величину абсолютных уровней .
В интервальных рядах динамики средний уровень у определяется делением суммы уровней  на их число n (формула 12):
на их число n (формула 12):
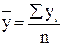 (12)
(12)
В моментном ряду динамики с равноотстоящими датами времени средний уровень определяется по формуле 13:
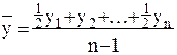 (13)
(13)
В моментном ряду динамики с неравноотстоящими датами средний уровень определяется по формуле 14:
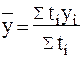 , (14)
, (14)
где 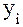 – уровни ряда динамики , сохранившиеся без изменения в течение промежутка времени
– уровни ряда динамики , сохранившиеся без изменения в течение промежутка времени 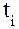 .
.
Средний абсолютный прирост представляет собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики . Для определения среднего абсолютного прироста 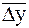 сумма цепных абсолютных приростов
сумма цепных абсолютных приростов 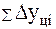 делится на их число n (формула 15):
делится на их число n (формула 15):
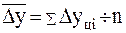 (15)
(15)
Средний абсолютный прирост может определяться по абсолютным уровням ряда динамики . Для этого определяется разность между конечным 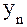 и базисным
и базисным 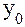 уровнями изучаемого периода , которая делится на m – 1субпериодов (формула 16):
уровнями изучаемого периода , которая делится на m – 1субпериодов (формула 16):
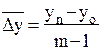 (16)
(16)
Основываясь на взаимосвязи между цепными и базисными абсолютными приростами , показатель среднего абсолютного прироста можно определить по формуле 17:
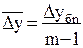 (17)
(17)
Средний темп роста – обобщающая характеристика индивидуальных темпов роста ряда динамики . Для определения среднего темпа роста 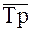 применяется формула 18:
применяется формула 18:
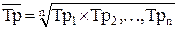 (18)
(18)
где Тр1 , Тр2 , ... , Трn -- индивидуальные (цепные) темпы роста (в коэффициентах), n -- число индивидуальных темпов роста.
Средний темп роста можно определить и по абсолютным уровням ряда динамики по формуле 19:
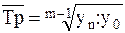 (19)
(19)
На основе взаимосвязи между цепными и базисными темпами роста средний темп роста можно определить по формуле 20:
 (20)
(20)
Средний темп прироста можно определить на основе взаимосвязи между темпами роста и прироста . При наличии данных о средних темпах роста для получения средних темпов прироста используется зависимость , выраженная формулой 21:
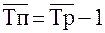 (21)
(21)
(при выражении среднего темпа роста в коэффициентах)
4. Проверка ряда на наличие тренда. Методы выделения тренда
Изучение тренда включает в себя два основных этапа :
1) Ряд динамики проверяется на наличие тренда
2) Производится выравнивание временного ряда и непосредственное выделение тренда с экстраполяцией полученных показателей – результатов .
Проверка на наличие тренда в ряду динамики может быть осуществлена по нескольким критериям .
1) Метод средних . Изучаемый ряд динамики разбивается на несколько интервалов (обычно на два) , для каждого из которых определяется средняя величина ( 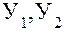 ) . Выдвигается гипотеза о существенном различии средних . Если эта гипотеза принимается , то признается наличие тренда .
) . Выдвигается гипотеза о существенном различии средних . Если эта гипотеза принимается , то признается наличие тренда .
2) Фазочастотный критерий знаков первой разности (критерий Валлиса и Мура) . Суть его заключается в следующем : наличие тренда в динамическом ряду утверждается в том случае , если этот ряд не содержит либо содержит в приемлемом количестве фазы – изменение знака разности первого порядка (абсолютного цепного прироста).
3) Критерий Кокса и Стюарта . Весь анализируемый ряд динамики разбивают на три равные по числу уровней группы (в том случае , когда число уровней ряда не делится на три , недостающие уровни надо добавить) и сравнивают между собой уровни первой и последней групп .
4) Метод серий . По этому способу каждый конкретный уровень временного ряда считается принадлежащим к одному из двух типов : например , если уровень ряда меньше медианного значения , то считается , что он имеет тип А , в противном случае – тип В. Теперь последовательность уровней выступает как последовательность типов . В образовавшейся последовательности типов определяется число серий (серия – любая последовательность элементов одинакового типа , с обоих сторон граничащая с элементами другого типа).
Если в ряду динамики общая тенденция к росту или снижению отсутствует , то количество серий является случайной величиной , распределенной приближенно по нормальному закону (для n > 10) . Следовательно , если закономерности в изменениях уровней нет , то случайная величина R оказывается в доверительном интервале
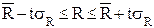 .
.
Параметр t назначается в соответствии с принятым уровнем доверительной вероятности Р.
Среднее число серий вычисляется по формуле 22 :
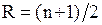 . (22)
. (22)
Среднее квадратическое отклонение числа серий вычисляется по формуле 23 :
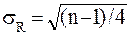 . (23)
. (23)
здесь n -- число уровней ряда .
Выражение для доверительного интервала приобретает вид
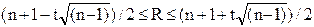
Полученные границы доверительного интервала округляют до целых чисел , уменьшая нижнюю границу и увеличивая верхнюю .
Непосредственное выделение трендаможет быть произведено тремя методами .
1) Укрупнение интервалов . Ряд динамики разделяют на некоторое достаточно большое число равных интервалов . Если средние уровни по интервалам не позволяют увидеть тенденцию развития явления , переходят к расчету уровней за большие промежутки времени , увеличивая длину каждого интервала (одновременно уменьшается количество интервалов) .
2) Скользящая средняя . В этом методе исходные уровни ряда заменяются средними величинами , которые получают из данного уровня и нескольких симметрично его окружающих . Целое число уровней , по которым рассчитывается среднее значение , называют интервалом сглаживания . Интервал может быть нечетным (3,5,7 и т.д. точек) или четным (2,4,6 и т.д. точек).
При нечетном сглаживании полученное среднее арифметическое значение закрепляют за серединой расчетного интервала , при четном это делать нельзя . Поэтому при обработке ряда четными интервалами их искусственно делают нечетными , для чего образуют ближайший больший нечетный интервал , но из крайних его уровней берут только 50%.
Недостаток методики сглаживания скользящими средними состоит в условности определения сглаженных уровней для точек в начале и конце ряда . Получают их специальными приемами – расчетом средней арифметической взвешенной . Так , при сглаживании по трем точкам выровненное значение в начале ряда рассчитывается по формуле 24 :
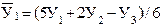 . (24)
. (24)
Для последней точки расчет симметричен .
При сглаживании по пяти точкам имеем такие уравнения (формулы 25):
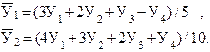 (25)
(25)
Для последних двух точек ряда расчет сглаженных значений полностью симметричен сглаживанию в двух начальных точках .
Формулы расчета по скользящей средней выглядят , в частности , следующим образом (формула 26):
для 3--членной 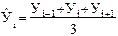 . (26)
. (26)
3) Аналитическое выравнивание . Под этим понимают определение основной проявляющейся во времени тенденции развития изучаемого явления . Развитие предстает перед исследователем как бы в зависимости только от течения времени . В итоге выравнивания временного ряда получают наиболее общий , суммарный , проявляющийся во времени результат действия всех причинных факторов . Отклонение конкретных уровней ряда от уровней , соответствующих общей тенденции , объясняют действием факторов , проявляющихся случайно или циклически . В результате приходят к трендовой модели , выраженной формулой 27:
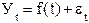 , (27)
, (27)
где f(t) – уровень , определяемый тенденцией развития ;
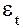 -- случайное и циклическое отклонение от тенденции.
-- случайное и циклическое отклонение от тенденции.
Целью аналитического выравнивания динамического ряда является определение аналитической или графической зависимости f(t) . На практике по имеющемуся временному ряду задают вид и находят параметры функции f(t) , а затем анализируют поведение отклонений от тенденции. Функцию f(t) выбирают таким образом , чтобы она давала содержательное объяснение изучаемого процесса .
Чаще всего при выравнивании используются следующий зависимости :
линейная 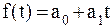 ;
;
параболическая 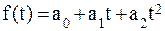 ;
;
экспоненциальная 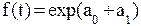
или 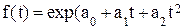 ).
).
1) Линейная зависимость выбирается в тех случаях , когда в исходном временном ряду наблюдаются более или менее постоянные абсолютные и цепные приросты , не проявляющие тенденции ни к увеличению , ни к снижению.
2) Параболическая зависимость используется , если абсолютные цепные приросты сами по себе обнаруживают некоторую тенденцию развития , но абсолютные цепные приросты абсолютных цепных приростов (разности второго порядка) никакой тенденции развития не проявляют .
3) Экспоненциальные зависимости применяются , если в исходном временном ряду наблюдается либо более или менее постоянный относительный рост (устойчивость цепных темпов роста , темпов прироста , коэффициентов роста) , либо , при отсутствии такого постоянства , -- устойчивость в изменении показателей относительного роста (цепных темпов роста цепных же темпов роста , цепных коэффициентов роста цепных же коэффициентов или темпов роста и т.д.).
Оценка параметров ( 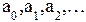 ) осуществляется следующими методами :
) осуществляется следующими методами :
1) Методом избранных точек,
2) Методом наименьших расстояний,
3) Методом наименьших квадратов (МНК)
В большинстве расчетов используется метод наименьших квадратов , который обеспечивает наименьшую сумму квадратов отклонений фактических уровней от выровненных :
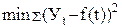 .
.
Для линейной зависимости ( 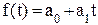 ) параметр
) параметр 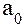 обычно интерпретации не имеет , но иногда его рассматривают , как обобщенный начальный уровень ряда ;
обычно интерпретации не имеет , но иногда его рассматривают , как обобщенный начальный уровень ряда ; 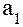 -- сила связи , т. е. параметр , показывающий , насколько изменится результат при изменении времени на единицу . Таким образом ,
-- сила связи , т. е. параметр , показывающий , насколько изменится результат при изменении времени на единицу . Таким образом , 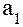 можно представить как постоянный теоретический абсолютный прирост .
можно представить как постоянный теоретический абсолютный прирост .
Построив уравнение регрессии , проводят оценку его надежности . Это делается посредством критерия Фишера (F) . Фактический уровень ( 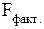 ) , вычисленный по формуле 28, сравнивается с теоретическим (табличным) значением :
) , вычисленный по формуле 28, сравнивается с теоретическим (табличным) значением :
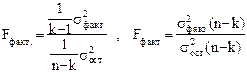 , (28)
, (28)
где k -- число параметров функции , описывающей тенденцию;
n -- число уровней ряда;
Остальные необходимые показатели вычисляются по формулам 29 – 31 :
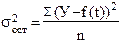 (29)
(29)
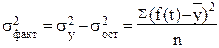 (30)
(30)
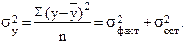 (31)
(31)
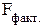 сравнивается с
сравнивается с 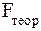 при
при 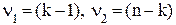 степенях свободы и уровне значимости a (обычно a = 0,05). Если
степенях свободы и уровне значимости a (обычно a = 0,05). Если 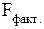 >
> 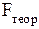 , то уравнение регрессии значимо , то есть построенная модель адекватна фактической временной тенденции.
, то уравнение регрессии значимо , то есть построенная модель адекватна фактической временной тенденции.
Дата добавления: 2017-04-20; просмотров: 771;
