Линии влияния внутренних усилий в сечениях трехшарнирной арки.

Построим линии влияния внутренних усилий в произвольном сечении 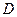трехшарнирной арки, используя статический метод. На рис.4.13,а показано сечение 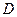, нормальное к оси арки, и.е. перпендикулярное к касательной, проведенной к оси арки в заданном сечении. Угол между касательной и горизонтальной прямой обозначим 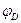. Расстояние от сечения до ближней опорной вертикали обозначим 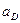, а его расстояние до дальней опорной вертикали обозначим .

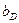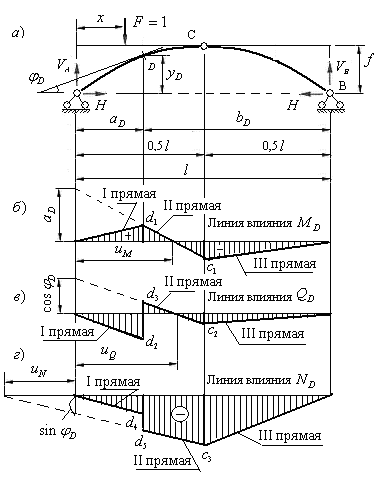
Рис.4.13

Установим силу 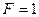на линию движения на переменном расстоянии 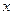от левой опорной вертикали и составим уравнения линий влияния внутренних усилий 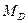, , 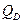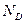. Очевидно, что эти усилия будут описываться различными уравнениями на трех участках движения силы :

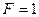- на участке между ближней опорной вертикалью и сечением;

- на участке между сечением и ключевым шарниром;

- на участке между ключевым шарниром и дальней опорной вертикалью.

Составим уравнение линии влияния 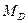, когда сила 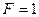находится на первом участке. В этом случае переменная 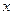меняется от нуля до 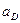, а справа от сечения действуют две силы – вертикальная реакция правой опоры 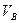и распор 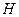. Эти реактивные силы на первом участке описываются уравнениями (4.22) и (4.23). Тогда:

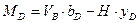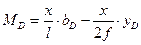, или (4.26)

Полученное уравнение является уравнением первой прямой линии влияния изгибающего момента в заданном сечении. Оно является линейным относительно переменной 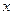, и его график легко построить по двум ординатам, вычисленным на границах участка:

- при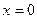

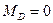
- при 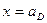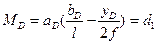(4.27)

Отложим ординату 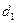вверх от нулевой прямой и соединим её с нулевой точкой под ближней опорой. В результате получим первую прямую (I прямую) линии влияния 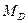(см. рис.4.13,б).

Переместим подвижную силу на второй участок и составим уравнение второй прямой, рассматривая равновесие левой осеченной части арки, которая загружена силам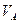и и 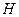. При этом учитываем, что 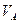изменяется согласно уравнению (4.21), а распор 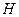- согласно уравнению (4,23). В результате получим:

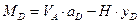, или 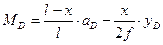(4.28)

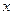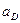Полученное уравнение справедливо в интервале изменения переменной от до 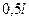. Вычисляем две ординаты линии влияния 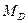на границах участка:

- при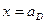

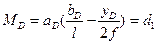
- при 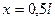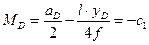(4.29)

Таким образом, под сечением ординаты первой прямой и второй прямой совпадают, следовательно, эти прямые пересекаются под сечением. Ордината второй прямой под ключевым шарниром всегда имеет знак минус. Откладываем величину 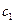вниз от нулевой прямой линии влияния 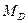. Через вершины двух ординат 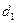и 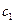проводим вторую прямую (см. рис.4.13,б). Эта прямая пересекает нулевую прямую линии влияния в некоторой точке, всегда расположенной между сечением и ключевым шарниром, и отстоящей на расстоянии 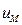от ближней опорной вертикали. Продолжение этой прямой отсекает на ближней опорной вертикале отрезок, численно равный расстоянию от сечения до этой вертикали, т.е. отрезок 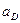. В этом легко убедиться, если в уравнение второй прямой (4.28) подставить .

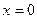Если подвижная сила 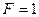перемещается на участке между ключевым шарниром арки и дальней опорной вертикалью, то уравнение третьей прямой также составляем из равновесия левой отсеченной части арки, но используем уравнение правой прямой линии влияния распора арки, т.е. уравнение (4.24).

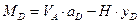, или 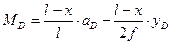(4.30)

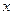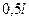Уравнение третьей прямой справедливо в интервале изменения переменной от до 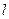. Вычисляем две ординаты третьей прямой:

- при 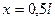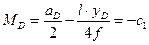(4.29)

- при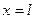

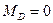
Таким образом, третья прямая проходит через нулевую точку под дальней опорой и пересекается со второй прямой под ключевым шарниром.

Анализируя полную линию влияния изгибающего момента в произвольном сечении 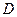трехшарнирной арки, легко установить следующие свойства:

1) Линия влияния изгибающего момента в любом сечении арки ограничена тремя прямыми: I прямой на участке между сечением и ближней опорной вертикалью; II прямой на участке между сечением и ключевым шарниром арки; III прямой между ключевым шарниром арки и дальней опорной вертикалью.

2) Каждая прямая имеет свою нулевую точку. Нулевая точка I прямой расположена под ближней опорой арки. Нулевая точка II прямой расположена на участке между сечением и ключевым шарниром и отстоит от ближней опорной вертикали на расстоянии 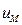. Продолжение II прямой отсекает на ближней опорной вертикали отрезок численно равный расстоянию от сечения до этой вертикали. (т.е. отрезок 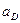, если сечение находится на левой полуарке, или отрезок 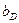, если сечение расположено на правой полуарке). Нулевая точка III прямой расположена под дальней опорой арки.

3) I и II прямые пересекаются под сечением арки, образуя максимальную ординату 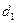, которая вычисляется по формуле (4.27) и всегда имеет знак плюс. II и III прямые пересекаются под ключевым шарниром арки, образуя минимальную ординату, которая вычисляется по формуле (4.29) и всегда имеет знак минус.

Приведенные свойства позволяют построить линию влияния изгибающего момента в любом сечении арки, не прибегая к составлению уравнений трех прямых.

Примечания:

1) Нумерация прямых, ограничивающих линию влияния на трех участках арки, осуществляется от ближней опоры по отношению сечения, т.е., если сечение находится на правой полуарке, то нумерацию прямых следует производить справа на лево;

2) Величину 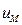, определяющую положение нулевой точки II прямой линии влияния 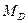легко выразить через известные величины 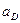и , и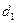спользуя пропорциональность сторон двух подобных треугольников.

На рис.4.14 представлены два подобных треугольника из линии влияния 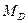. Запишем пропорциональность их сторон:

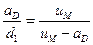
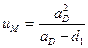(4.30)

Если сечение задано на правой полуарке, то расстояние 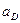необходимо заменить расстоянием .

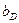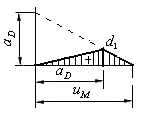
Рис.4.14

Величину 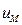можно определить, используя теорему о трех силах. Нулевая точка II прямой линии влияния 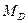определяет положение подвижной силы 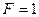, при котором в заданном сечении трехшарнирной арки изгибающий момент равен нулю. Тогда линия действия реакции ближней опоры должна проходить через центр сечения, а линия действия реакции дальней опоры должна проходить через ключевой шарнир арки. Согласно теореме о трех силах, линии действия указанных сил пересекаются в одной точке О (рис.4.15).

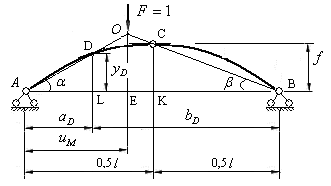
Рис.4.15

Найдем отрезок OE из двух треугольников:

- из треугольника AOE:

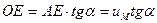(4.31)

- из треугольника OBE:

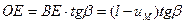(4.32)

Приравнивая правые части выражений (4.31) и (4.32), получим:

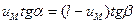, откуда

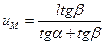, (4.33)

где: 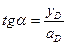- для сечений на левой полуарке и

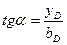- для сечений на правой полуарке,

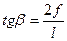независимо от расположения сечения.

Расстояние 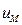нулевой точки II прямой линии влияния

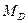, можно вычислять по формулам (4.30) и (4.33). Результаты всегда совпадают.

Составим уравнения трех прямых, ограничивающих линию влияния поперечной силы в заданном сечении 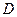трехшарнирной арки.

Если сила 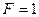перемещается на участке между ближней опорой и сечением, то переменная 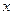меняется от нуля до 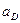. Проецируя правые силы, относительно заданного сечения, на направление нормали к оси арки в этом сечении и, учитывая правило знаков поперечной силы, получим уравнение I прямой:

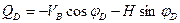, или 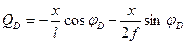(4.34)

Вычисляем две ординаты I прямой:

- при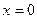

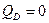
- при 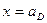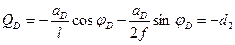(4.35)

Отложим эту ординату вниз от нулевой прямой и соединим её вершину с нулевой точкой под ближней опорой, получим I прямую (рис.4.33,в).

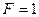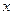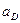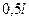Если сила перемещается на участке между сечением и ключевым шарниром, то переменная меняется от до . Проецируя левые силы, относительно заданного сечения, на направление нормали к оси арки в этом сечении и, учитывая правило знаков поперечной силы, получим уравнение II прямой:

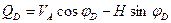, или 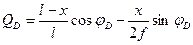(4.36)

Вычисляем две ординаты II прямой:

- при 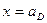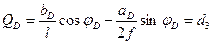(4.37)

- при 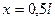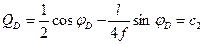(4.38)

Ордината 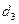имеет знак плюс. Откладываем её вверх от нулевой прямой. Разность ординат 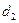и 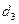, вычисленных по формулам (4.35) и (4.37), равна: 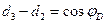. Это означает, что при расположении силы 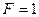над сечением арки, поперечная сила претерпевает разрыв на величину равную .

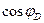В зависимости от расположения сечения ордината 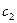может иметь положительное, отрицательное или нулевое значение. На рис.4.33,в ордината 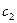принята с отрицательным знаком и отложена вниз от нулевой прямой. Тогда II прямая линии влияния поперечной силы пересечет нулевую прямую на участке между сечением и ключевым шарниром арки.

Найдем величину отрезка, который отсекает продолжение II прямой на ближней опорной вертикали. Для этого в уравнение (4.36) подставим 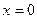, получим 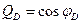. Легко заметить, что полученное значение равно разности ординат 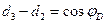под сечением. Это означает, что II прямая линии влияния поперечной силы параллельна I прямой.

При движении силы 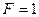на участке между ключевым шарниром и дальней опорной вертикалью, уравнение III прямой составляем, проецируя левые силы на направление нормали к оси арки в заданном сечении. В результате получим:

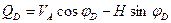, или 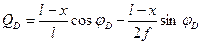(4.39)

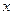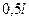Уравнение III прямой справедливо в интервале изменения от до 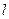. Вычисляем две ординаты этой прямой на границах участка:

- при 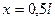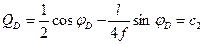(4.40)

- при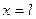

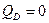
Таким образом, III прямая линии влияния 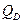, проходит из вершины ординаты 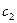в нулевую точку под дальней опорой.

Анализируя построенную линию влияния поперечной силы в произвольном сечении арки, легко установить следующие её свойства:

1) Она ограничена тремя прямыми: I прямой – на участке между ближней опорой арки и заданным сечением; II прямой – на участке между сечением и ключевым шарниром арки; III прямой – на участке между ключевым шарниром и дальней опорой.

2) I прямая линии влияния поперечной силы параллельна II прямой, а продолжение II прямой отсекает на ближней опорной вертикали отрезок, численно равный 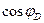. При этом для сечений, расположенных на левой полуарке указанный отрезок откладывают на левой опорной вертикали вверх от нулевой прямой. Для сечений, расположенных на правой полуарке, указанный отрезок откладывают на правой опорной вертикали вниз от нулевой прямой. (В силу того, что поперечная сила является косо симметричным усилием в отличие от изгибающего момента или продольной силы).

3) I прямая проходит через нулевую точку под ближней опорой, II прямая проходит через нулевую точку, расположенную внутри пролета арки и отстоящую от ближней опорной вертикали на расстоянии 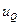. III проходит через нулевую точку под дальней опорой.

Величина 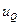может быть вычислена двумя способами, аналогично вычислению величины 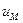, т.е. из подобия треугольников линии влияния 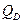, или по теореме о трех силах. Опуская вывод, приводим формулы для определения .

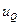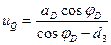, где (4.41)

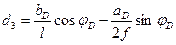
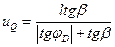(4.42)

Аналогично составляются уравнения трех прямых линии влияния продольной силы 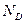и осуществляется построение линии влияния. Предлагаем студентам, изучающим курс строительной механики, составить указанные уравнения трех прямых и построить линию влияния продольной силы .

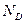На рис.4.13,г построена линия влияния продольной силы для заданного сечения, расположенного на левой полуарке. Сформулируем свойства этой линии влияния, а также приведем без вывода уравнения прямых и формулы для вычисления ординат линии влияния под сечением и ключевым шарниром.

1) Линия влияния продольной силы ограничена тремя прямыми: I прямой – на участке между ближней опорой арки и заданным сечением; II прямой – на участке между сечением и ключевым шарниром арки; III прямой – на участке между ключевым шарниром и дальней опорой.

Уравнение I прямой: 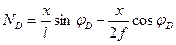(4.43)

Уравнение II прямой: 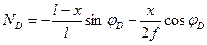(4.44)

Уравнение III прямой: 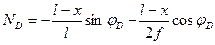(4.45)

Ордината I прямой под сечением:

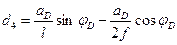(4.46)

Ордината II прямой под сечением:

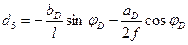(4.47)

Ордината II прямой под ключевым шарниром:

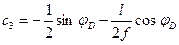(4.48)

2) I прямая линии влияния продольной силы проходит через нулевую точку под ближней опорой параллельно II прямой. III проходит через нулевую точку под дальней опорой. Продолжение II прямой пересекается с продолжением нулевой прямой в точке, которая расположена на расстоянии 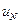от ближней опорной вертикали (см. рис.4.33,г).

В отличие от линий влияния изгибающего момента и поперечной силы, нулевая точка II прямой линии влияния продольной силы находится вне пролета арки со стороны ближней опорной вертикали.

3) Продолжение II прямой отсекает на ближней опорной вертикали отрезок, равный 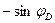. Независимо от расположения сечения арки, этот отрезок откладывают вниз от нулевой прямой на ближней опорной вертикали.

Величина 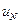может быть вычислена двумя способами, аналогично вычислению величины 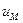, т.е. из подобия треугольников линии влияния 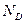, или по теореме о трех силах. Опуская вывод, приводим формулы для определения .

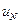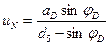, (4.49)

где 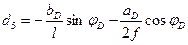по формуле (4.47)

или 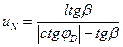(4.50)

Изложенный выше статический метод построения линий влияния дает возможность составить уравнения прямых, которые ограничивают линии влияния внутренних усилий в заданном сечении арки на трех участках и построить их графики, т.е. линии влияния.

При построении линий влияния для конкретно заданной трехшарнирной арки нет необходимости составлять уравнения трех прямых. Достаточно вычислить расстояния от нулевых точек второй прямой линий влияния 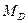, 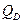и 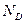по формулам (4.33), (4.42) и (4.50) и использовать сформулированные выше свойства прямых, ограничивающих линии влияния на отдельных участках. Либо вычислить ординаты прямых под сечением и ключевым шарниром по приведенным выше формулам.

Пример 4.2 Для трехшарнирной арки (рис.4.16,а) требуется построить линии влияния усилий в заданных сечениях 1 и 2, вычислить усилия по линиям влияния от неподвижных нагрузок, представленных на рис.4.16,б и сравнить их с величинами, полученными аналитическим методом (см. пример 4.1). Для расчета принять: , , , .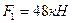

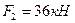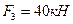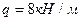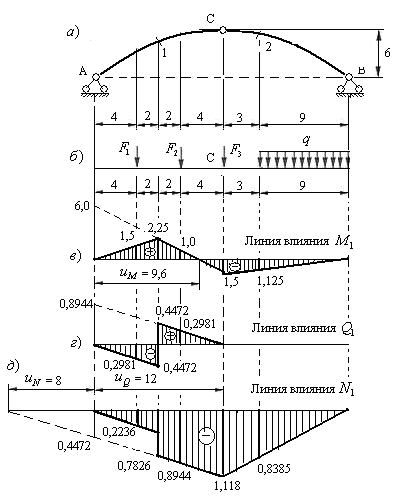
Рис.4.16

Решение. 1) Строим линию влияния изгибающего момента в сечении 1 арки. Для этого:

- Определяем величину 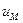по формуле (4.33)

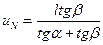
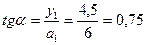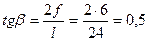, , тогда: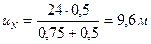

- Проводом нулевую прямую линии влияния 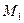(рис.4.16,в) и откладываем на ней внутрь пролета арки величину 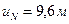в масштабе длин. В результате получаем нулевую точку второй прямой.

- Откладываем на левой опорной вертикали, вверх от нулевой прямой, отрезок равный 6 м. и через его вершину и нулевую точку проводим II прямую линии влияния 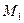и ограничиваем её ординатами под сечением и ключевым шарниром. Величины указанных ординат вычисляем из подобия треугольников:

Ордината под сечением равна 6х3,6:9,6=2,25

Ордината под ключевым шарниром равна -6х2,4:9,6=-1,5

Проверим величины этих ординат, используя формулы (4.27) и (4.29)

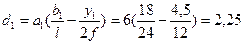
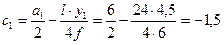
- Вершину ординаты II прямой под сечением (равную 2,25) соединяем с нулевой точкой под левой опорой (I прямая), а вершину ординаты той же прямой под ключевым шарниром (равную -1,5) соединяем с нулевой точкой под правой опорой (III прямая). Получаем линию влияния изгибающего момента в сечении 1.

Загрузим линию влияния 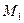нагрузками, показанными на рис.4.16,б. Вычислим дополнительно ординаты линии влияния под силами и на левой границе распределенной нагрузки, используя подобные треугольники (величины и знаки этих ординат указаны на рис.4.16,в), и вычислим изгибающий момент .

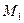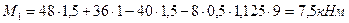
В примере 4.1 вычислена величина 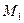аналитическим методом, и она полностью совпадает с величиной, вычисленной по линии влияния.

2) Строим линию влияния поперечной силы в сечении 1 арки в той же последовательности, что и линию влияния изгибающего момента. Для этого:

- Определяем величину 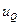по формуле (4.42)

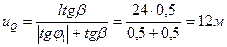
- Проводом нулевую прямую линии влияния 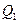(рис.4.16,г) и откладываем на ней внутрь пролета арки величину 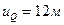в масштабе длин. В результате получаем нулевую точку второй прямой, расположенную под ключевым шарниром арки. Для проверки вычислим ординату линии влияния под ключевым шарниром по формуле (4.40):

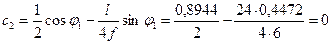
- Откладываем на левой опорной вертикали, вверх от нулевой прямой, отрезок равный 0,8944 и через его вершину и нулевую точку проводим II прямую линии влияния .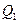

Ограничиваем её ординатой под сечением и вычисляем эту ординату из подобия треугольников: 0,8944 х 6:12=0,4472. Эту ординату можно вычислить по формуле (4.37):

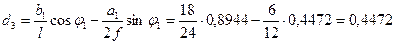
Из нулевой точки л.в. 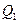под левой опорой проводим

I прямую параллельно II прямой, ограничиваем её ординатой под сечением и вычисляем эту ординату:

0,8944- 0,4472=0,4472 .

Эту ординату можно вычислить по формуле (4.35):

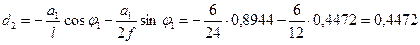
Загрузим линию влияния 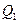нагрузками, показанными на рис.4.16,б. Вычислим дополнительно ординаты линии влияния под силам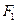и и 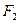, используя подобные треугольники: ордината под силой 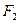равна 0,4472х4:6=0,2981, ордината под силой 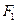равна -0,4472х4:6=-0,2981. Вычислим поперечную силу .

.

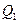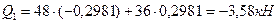Полученное значение поперечной силы 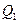полностью совпадает со значением 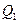, вычисленным аналитическим методом в примере 4.1.

3) Строим линию влияния продольной силы в сечении 1 арки в той же последовательности, что и линию влияния поперечной силы. Для этого:

- Определяем величину 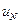по формуле (4.50)

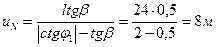
- Проводом нулевую прямую линии влияния 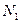(рис.4.16,д) и продлеваем её влево от ближней (левой) опорной вертикали на величину 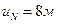в масштабе длин. В результате получаем нулевую точку второй прямой, расположенную вне пролета арки.

- Откладываем на левой опорной вертикали, вниз от нулевой прямой, отрезок равный -0,4472 и через его вершину и нулевую точку проводим II прямую линии влияния .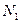

Ограничиваем её ординатами под сечением и ключевым шарниром арки. Вычисляем эти ординаты из подобия треугольников:

Ордината под сечением равна -0,4472 х 14:8=-0,7826.

Ордината под ключевым шарниром равна:

-0,4472 х 20:8=-1,118

Эти ординату можно вычислить по формулам (4.47) и (4.48):

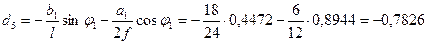
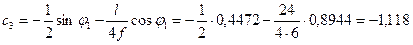
Из нулевой точки л.в. 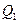под левой опорой проводим

I прямую параллельно II прямой, ограничиваем её ординатой под сечением и вычисляем эту ординату:

-0,7826-(-4472)=-0,3354 .

Эту ординату можно вычислить по формуле (4.46):

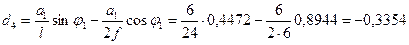
Загрузим линию влияния 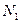нагрузками, показанными на рис.4.16,б. Вычислим дополнительно ординаты линии влияния под всеми силами и на левой границе распределенной нагрузки, используя подобные треугольники: Величины этих ординат приведены на рис.4.16,д. Вычислим продольную силу .

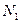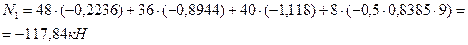
Полученное значение поперечной силы 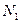полностью совпадает со значением 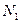, вычисленным аналитическим методом в примере 4.1.

Построим линии влияния усилий в сечении 2, расположенном на правой полуарке, используя их свойства (рис.4.17). Напомним, что нумерация прямых, ограничивающих линии влияния проводится всегда от ближней к сечению опоры. Для сечения 2 прямые линий влияния усилий нумеруем справа налево. Положения нулевых точек вторых прямых линий влияния определяются по формулам (4.33), (4.42) и (4.44), как и для сечений, расположенных на левой полуарке, но откладывают их от правой опорной вертикали.

Вычислим величину :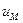

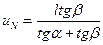, где ,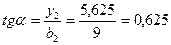

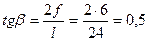, тогда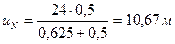

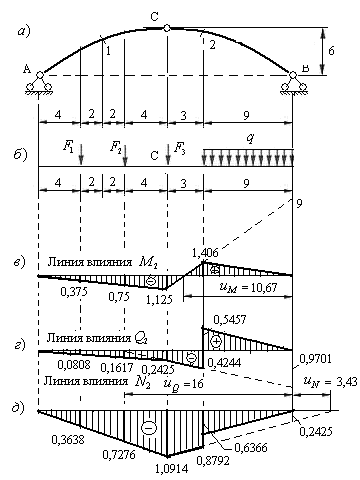
Рис.4.17

Проводим нулевую прямую линии влияния 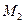и откладываем на ней внутрь пролета арки величину 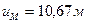. Получаем нулевую точку второй прямой.

Откладываем на правой опорной вертикали, вверх от нулевой прямой, отрезок равный 9 м. и через его вершину и нулевую точку проводим II прямую линии влияния 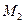. Ограничиваем её ординатами под сечением и ключевым шарниром. Величины указанных ординат вычисляем из подобия треугольников:

Ордината под сечением равна: 9х1,67:10,67=1,406

Ордината под ключевым шарниром равна:

-9х1,33:10,67=-1,125. Вычислим дополнительно ординаты линии влияния под силам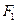и и 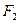. Ордината под силой 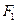равна -1,125х4:12=-0,375, ордината под силой 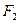равна -1,125х8:12=-0,75. Определяем изгибающий момент 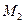по линии влияния:

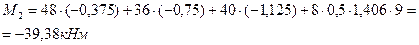
В примере 4.1 изгибающий момент вычислен аналитическим методом и он полностью совпадает со значением 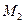, вычисленным по линии влияния.

Строим линию влияния поперечной силы в сечении 2 арки в той же последовательности, что и линию влияния изгибающего момента. Для этого:

- Определяем величину 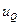по формуле (4.42)

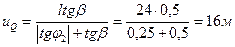
- Проводом нулевую прямую линии влияния 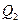(рис.4.17,г) и откладываем на ней от правой опорной вертикали внутрь пролета арки величину 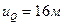в масштабе длин. В результате получаем нулевую точку второй прямой, расположенную слева от ключевого шарнира.

- Откладываем на левой опорной вертикали, вниз от нулевой прямой, отрезок равный - 0,9701 и через его вершину и нулевую точку проводим II прямую линии влияния .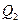

Ограничиваем её ординатами под сечением и ключевым шарниром и вычисляем эти ординаты из подобия треугольников:

Ордината под сечением равна: – 0,9701 х7:16=- 0,4244

Ордината под ключевым шарниром равна:

– 0,9701 х4:16=- 0,24254.

Из нулевой точки л.в. 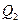под правой опорой проводим

I прямую параллельно II прямой, ограничиваем её ординатой под сечением и вычисляем эту ординату:

0,9701- 0,4244=0,5457 .

Загрузим линию влияния 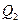нагрузками, показанными на рис.4.17,б. Вычислим дополнительно ординаты линии влияния под силам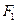и и 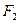, используя подобные треугольники: ордината под силой 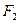равна -0,24254х8:12=-0,1617, ордината под силой 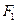равна -0,24254х4:12=-0,08084. Вычислим поперечную силу .

.

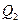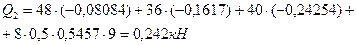Сопоставляем эту величину с величиной 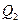, вычисленной аналитическим методом в примере 4.1. 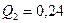. Расхождение между двумя величинами составляет менее 1%. (Допускается до 5%).

Строим линию влияния продольной силы в сечении 2 арки в той же последовательности, что и линию влияния поперечной силы. Для этого:

- Определяем величину 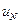по формуле (4.50)

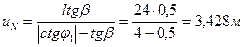
- Проводом нулевую прямую линии влияния 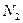(рис.4.17,д) и продлеваем её вправо от ближней (правой) опорной вертикали на величину 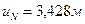в масштабе длин. В результате получаем нулевую точку второй прямой, расположенную вне пролета арки.

- Откладываем на правой опорной вертикали, вниз от нулевой прямой, отрезок равный -0,2425 ( 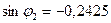) и через его вершину и нулевую точку проводим II прямую линии влияния .

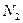Ограничиваем её ординатами под сечением и ключевым шарниром арки. Вычисляем эти ординаты из подобия треугольников:

Ордината под сечением равна

-0,2425 х 12,428:3,428=-0,8792.

Ордината под ключевым шарниром равна:

-0,2425 х 15,428:3,428=-1,0914.

Вычислим дополнительно ординаты линии влияния 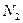под силам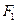и и 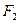, используя подобные треугольники: ордината под силой 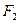равна -1,0914х8:12=-0,7276, ордината под силой 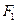равна -1,0914х4:12=-0,3638. Вычислим величину продольной силы 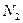по линии влияния от действия заданных нагрузок.

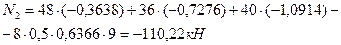
Это значение полностью совпадает со значением 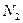, вычисленным в примере 4.1 аналитическим методом.

Вопросы для самоконтроля полученных знаний.

1. Какие системы называют распорными?

2. Назовите основные элементы трехшарнирной арки.

3. Приведите типы трехшарнирных арок в зависимости от очертания оси, наличия затяжки, расположения пят.

4. Какие уравнения равновесия используются для определения опорных «реакций?

5. Как зависит распор при действии вертикальной нагрузки от стрелы подъема арки?

6. Как записывается выражение изгибающего момента в сечении арки от вертикальной нагрузки?

7. Как получают выражения для определения поперечной и продольной сил в сечении арки от вертикальной нагрузки?

8. Чем отличаются усилия в арке от балочных усилий?

9. Как зависят изгибающие моменты при действии вертикальной нагрузки

10. от стрелы подъема?

11. Чем отличается характер эпюры внутренних усилий в арке от балочных ,эпюр?

12. В чем заключаются особенности расчета арки с затяжкой?

13. Когда рационально применять в сооружениях арки с затяжкой?

14. В чем состоит особенность работы частей арки, расположенных ниже повышенной затяжки?

15. Отличаются ли линии влияния вертикальных составляющих опорных реакций в трехшарнирной арке от балочных реакций?

16. Как построить линии влияния усилий в сечении арки способом наложения?

17. Как построить линии влияния усилий в сечении арки с помощью нулевых точек?

18. Как найти положение нулевых точек?

19. Сколько линейных участков содержат линии влияния внутренних усилий в сечении арки?

20. Как определяют наибольшие (наименьшие) нормальные напряжения в сечении арки?

21. В чем заключаются особенности вычисления реакций и усилий в трехшарнирных арках при действии произвольно направленной нагрузки?