АНАЛИЗ ВНУТРЕННИХ СИЛОВЫХ ФАКТОРОВ

При изучении классификации внешних сил (нагрузок) следует отчетливо представлять их разновидности в зависимости от способа их приложения – объемные и поверхностные. Поверхностные нагрузки делят на распределенные и сосредоточенные. По характеру действия нагрузки делят на статические и динамические. Необходимо разбираться в разновидностях каждой из нагрузок и суметь привести пример на каждую из них.

Нагрузки, действующие на тело, вызывают в нем деформации. Тело, деформации которого рассматриваются, имеет форму бруса, т.е. тела, у которого длина значительно больше линейных размеров поперечного сечения. Если деформация после прекращения действия сил на тело исчезает, то такая деформация называется упругой. Неисчезающие деформации называются остаточными или пластическими, такие деформации в машинах и сооружениях, как правило, не допускаются.

Внешние силы (нагрузки), действующие на брус, вызывают возникновение в нем внутренних сил (сил упругости). Для определения внутренних сил пользуются методом сечений, который позволяет определить внутренние силы в том или ином сечении тела, и заключается в следующем: брус, находящийся в равновесии, разрезают (мысленно) на две части, отбрасывают одну из частей, заменяют действие отброшенной части на оставшуюся внутренними силами и составляют уравнения равновесия для оставшейся части, на которую действуют приложенные к ней внешние и внутренние силы. Действующая в проведенном поперечном сечении система внутренних сил эквивалентна в общем случае одной силе и одному моменту. Разложив их на составляющие, получим соответствующие три силы (по направлению координатных осей Q_x, Q_y, N_z) и три момента (относительно этих осей М_х, М_y, M_z), которые называют внутренними силовыми факторами (ВСФ)

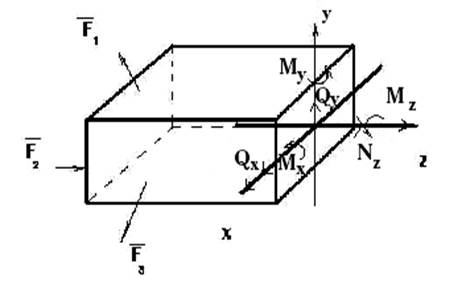
Рисунок 1- Распределение ВСФ

Возникновение тех или иных ВСФ зависит от фактического нагружения бруса. Определяют ВСФ с помощью уравнений равновесия статики (рисунок 1).

1 ∑F_ix=0 4 ∑M_x(F_i)=0

2 ∑F_iy=0 5 ∑M_y(F_i)=0

3 ∑F_iz=0 6 ∑M_z(F_i)=0

Надо хорошо усвоить, что внутренним нормальным силам соответствуют нормальные напряжения – σ (сигма), касательным силам касательные напряжения – τ (тау). Рисунок 2.

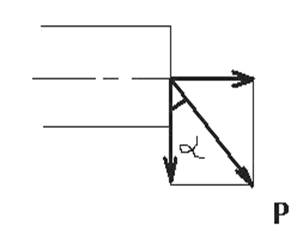
Рисунок 2- Распределение напряжений по сечению

Нормальное напряжение σ, действующее нормально, т.е. перпендикулярно к сечению, и касательное напряжение τ, действующее параллельно плоскости сечения или касательно к нему, являются составляющими полного напряжения р, величина которого равна: 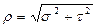Напряжение выражает меру внутренних сил, возникающих в материале элемента конструкции.