Аналитический метод определения реакций опор трехшарнирной арки.

Рассмотрим трехшарнирную арку, загруженную системой вертикальных сосредоточенных сил 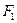, ,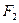… 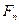(рис.4.8,а) и однопролетную балку на двух шарнирных опорах, имеющую тот же пролет и загруженную теми же нагрузками, что и арка (рис.4.8,б).

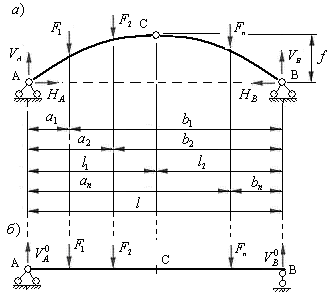
Рис.4,8

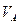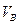Обе опоры трехшарнирной арки шарнирно неподвижные и в них возникают по две составляющие реакций: вертикальные и горизонтальные. Обозначим вертикальные составляющие буквами и , а горизонтальные составляющие буквам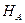и и .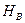

В опорах балки при вертикальных нагрузках возникают только вертикальные реакци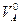и, и 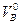. Определим сначала вертикальные реакции опор балки из условий её равновесия относительно опорных шарниров:

_,

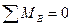
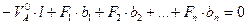Откуда 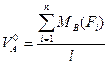(4.7)

_,

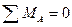
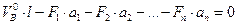Откуда 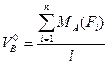(4.8)

Определим внутренние усилия в сечении С балки, расположенном под ключевым шарниром арки. Эти усилия будем называть балочными усилиями, т.е балочной поперечной силой в сечении балки под ключевым шарниром арки:

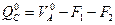(4.9)

и балочным изгибающим моментом в том же сечении:

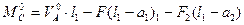(4.10)

Перейдем к определению реакций опор трехшарнирной арки.

Для определения четырех неизвестных реакций опор арки, показанных на рис.4.8,а необходимо составить четыре уравнения. Три из них составляем из условий равновесия арки в целом, а четвертое – из условия равновесия одной полуарки по отношению к другой. Такое равновесие возможно, если изгибающий момент в ключевом шарнире арки равен нулю. Запишем условия равновесия, составим уравнения равновесия и найдем все составляющие реакций опор арки из их решения:

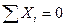
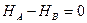
1) 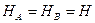(1.11)

Из равенства (1.11) следует, что при загружении арки вертикальными нагрузками горизонтальные составляющие реакций опор равны по модулю и противоположно направлены внутрь пролета арки. Они называются распором арки. Эти силы удерживают опоры арки на заданном расстоянии.

2) _,

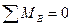
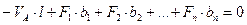Откуда 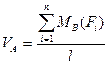(4.12)

3) _,

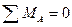
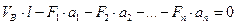Откуда 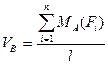(4.13)

Сопоставляя выражения (4.7) с (4.12) и (4.8) с (4.13) легко заметить, что вертикальные составляющие реакций опор арки и балки одинаковы, если балка имеет тот же пролет и несет те же нагрузки, что и арка.

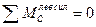
4) 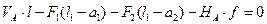(4.14)

Учитывая, что 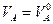, а 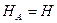и используя выражение (4.10), равенство (4.14) приведем к виду:

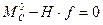, откуда

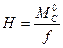(4.15)

Таким образом, распор арки равен отношению балочного изгибающего момента в сечении, взятом под ключевым шарниром арки к стреле подъема арки.